Câu hỏi: Tam giác \(ABC\) vuông cân tại \(A\) và nội tiếp trong đường tròn tâm \(O\) bán kính \(R\). Gọi \(r\) là bán kính đường tròn nội tiếp tam giác \(ABC\). Khi đó tỉ số \({R \over r}\) là:
A. \(1 + \sqrt 2\)
B. \({{2 + \sqrt 2 } \over 2}\)
C. \({{\sqrt 2 - 1} \over 2}\)
D. \({{1 + \sqrt 2 } \over 2}\)
A. \(1 + \sqrt 2\)
B. \({{2 + \sqrt 2 } \over 2}\)
C. \({{\sqrt 2 - 1} \over 2}\)
D. \({{1 + \sqrt 2 } \over 2}\)
Phương pháp giải
- Tính bán kính R.
- Tính diện tích tam giác và nửa chu vi suy ra r.
- Tính tỉ số.
Lời giải chi tiết
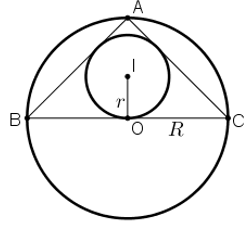
Đặt AB=AC=a.
+) Tam giác ABC vuông tại A nên theo Pitago ta có: \(BC =AB^2+AC^2\) \(= \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
\(\Rightarrow R =\frac{1}{2}BC= \frac{{a\sqrt 2 }}{2}.\)
+) Nửa chu vi tam giác \(ABC\) là: \(p = \frac{{a + a + a\sqrt 2 }}{2}\) \(= \frac{{2a + a\sqrt 2 }}{2}\)
Ta có: \({S_{ABC}} = \frac{1}{2}AB. AC = \frac{1}{2}. A. A = \frac{{{a^2}}}{2}\)
Mà \({S_{ABC}} = pr\)
\(\Rightarrow r = \frac{{{S_{ABC}}}}{p} = \frac{{\frac{{{a^2}}}{2}}}{{\frac{{2a + a\sqrt 2 }}{2}}} \) \(= \frac{{{a^2}}}{2}:\frac{{2a + a\sqrt 2 }}{2} = \frac{{{a^2}}}{2}.\frac{2}{{2a + a\sqrt 2 }} = \frac{a}{{2 + \sqrt 2 }}\)
\(\Rightarrow \frac{R}{r}\) \( = \frac{{\frac{{a\sqrt 2 }}{2}}}{{\frac{a}{{2 + \sqrt 2 }}}}\)
\(= \frac{{a\sqrt 2 }}{2}:\frac{a}{{2 + \sqrt 2 }} = \frac{{a\sqrt 2 }}{2}.\frac{{2 + \sqrt 2 }}{a}\) \(= \frac{{\sqrt 2 \left( {2 + \sqrt 2 } \right)}}{2} = \sqrt 2 + 1\)
Vậy chọn A.
- Tính bán kính R.
- Tính diện tích tam giác và nửa chu vi suy ra r.
- Tính tỉ số.
Lời giải chi tiết
Đặt AB=AC=a.
+) Tam giác ABC vuông tại A nên theo Pitago ta có: \(BC =AB^2+AC^2\) \(= \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
\(\Rightarrow R =\frac{1}{2}BC= \frac{{a\sqrt 2 }}{2}.\)
+) Nửa chu vi tam giác \(ABC\) là: \(p = \frac{{a + a + a\sqrt 2 }}{2}\) \(= \frac{{2a + a\sqrt 2 }}{2}\)
Ta có: \({S_{ABC}} = \frac{1}{2}AB. AC = \frac{1}{2}. A. A = \frac{{{a^2}}}{2}\)
Mà \({S_{ABC}} = pr\)
\(\Rightarrow r = \frac{{{S_{ABC}}}}{p} = \frac{{\frac{{{a^2}}}{2}}}{{\frac{{2a + a\sqrt 2 }}{2}}} \) \(= \frac{{{a^2}}}{2}:\frac{{2a + a\sqrt 2 }}{2} = \frac{{{a^2}}}{2}.\frac{2}{{2a + a\sqrt 2 }} = \frac{a}{{2 + \sqrt 2 }}\)
\(\Rightarrow \frac{R}{r}\) \( = \frac{{\frac{{a\sqrt 2 }}{2}}}{{\frac{a}{{2 + \sqrt 2 }}}}\)
\(= \frac{{a\sqrt 2 }}{2}:\frac{a}{{2 + \sqrt 2 }} = \frac{{a\sqrt 2 }}{2}.\frac{{2 + \sqrt 2 }}{a}\) \(= \frac{{\sqrt 2 \left( {2 + \sqrt 2 } \right)}}{2} = \sqrt 2 + 1\)
Vậy chọn A.
Đáp án A.