Câu hỏi: Chứng minh rằng diện tích của một tứ giác bằng nửa tích hai đường chéo và sin của góc hợp bởi hai đường chéo đó.
Phương pháp giải
- Chia tứ giác ABCD thành 4 tam giác nhỏ để tính diện tích mỗi tam giác đó.
- Cộng các kết quả với nhau suy ra đpcm.
Sử dụng công thức diện tích tam giác $S = \dfrac{1}{2}ab\sin C$
Lời giải chi tiết
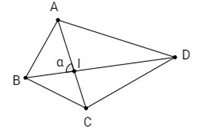
Gọi \(I\) là giao điểm của hai đường chéo \(AC, BD\) và \(\widehat {AIB} = \alpha \).
Ta có \({S_{ABI}} = {1 \over 2}AI. BI.\sin \alpha \)
\({S_{ADI}} = {1 \over 2}AI. DI.\sin ({180^0} - \alpha) \)
\(= {1 \over 2}AI. DI.\sin \alpha \)
(hai góc bù nhau có sin bằng nhau)
Suy ra \({S_{ABD}} = {S_{ABI}} + {S_{ADI}} \)
\(= \frac{1}{2}AI. BI.\sin \alpha + \frac{1}{2}AI. DI.\sin \alpha \)
\(= {1 \over 2}AI.(BI + DI).\sin \alpha \)
\(= {1 \over 2}AI. BD.\sin \alpha \)
Tương tự ta suy ra:
\({S_{BCD}} = {S_{BIC}} + {S_{CDI}}\)\(= {1 \over 2}CI. BD.\sin \alpha \)
Do đó,
\({S_{ABCD}} = {S_{ABD}} + {S_{BCD}}\)
\(= \frac{1}{2}AI. BD.\sin \alpha + \frac{1}{2}CI. BD.\sin \alpha \)
\(= {1 \over 2}. BD.(AI + CI).\sin \alpha \)
\(= {1 \over 2}. BD. AC.\sin \alpha. \)
- Chia tứ giác ABCD thành 4 tam giác nhỏ để tính diện tích mỗi tam giác đó.
- Cộng các kết quả với nhau suy ra đpcm.
Sử dụng công thức diện tích tam giác $S = \dfrac{1}{2}ab\sin C$
Lời giải chi tiết
Gọi \(I\) là giao điểm của hai đường chéo \(AC, BD\) và \(\widehat {AIB} = \alpha \).
Ta có \({S_{ABI}} = {1 \over 2}AI. BI.\sin \alpha \)
\({S_{ADI}} = {1 \over 2}AI. DI.\sin ({180^0} - \alpha) \)
\(= {1 \over 2}AI. DI.\sin \alpha \)
(hai góc bù nhau có sin bằng nhau)
Suy ra \({S_{ABD}} = {S_{ABI}} + {S_{ADI}} \)
\(= \frac{1}{2}AI. BI.\sin \alpha + \frac{1}{2}AI. DI.\sin \alpha \)
\(= {1 \over 2}AI.(BI + DI).\sin \alpha \)
\(= {1 \over 2}AI. BD.\sin \alpha \)
Tương tự ta suy ra:
\({S_{BCD}} = {S_{BIC}} + {S_{CDI}}\)\(= {1 \over 2}CI. BD.\sin \alpha \)
Do đó,
\({S_{ABCD}} = {S_{ABD}} + {S_{BCD}}\)
\(= \frac{1}{2}AI. BD.\sin \alpha + \frac{1}{2}CI. BD.\sin \alpha \)
\(= {1 \over 2}. BD.(AI + CI).\sin \alpha \)
\(= {1 \over 2}. BD. AC.\sin \alpha. \)