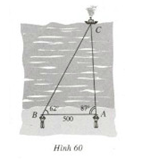
Câu hỏi: Hình 60 vẽ một chiếc tàu thủy đang neo đậu ở vị trí \(C\) trên biển và hai người ở các vị trí quan sát \(A\) và \(B\) cách nhau \(500m\). Họ đo được góc \(CAB\) bằng \({87^0}\) và góc \(CBA\) bằng \({62^0}\).
Tính các khoảng cách \(AC\) và \(BC\).
Tính các khoảng cách \(AC\) và \(BC\).

Phương pháp giải
- Tính C dựa vào công thức A+B+C=180
- Sử dụng định lí sin tính AC, BC:
\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}}\)
Lời giải chi tiết
Ta có \(\widehat {ACB} = {180^0} - \widehat {BAC} - \widehat {ABC}\) \(= {180^0} - {87^0} - {62^0} = {31^0}\)
Áp dụng định lí sin ta có
\(\begin{array}{l}
\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}} \Rightarrow \frac{{500}}{{\sin {{31}^0}}} = \frac{{BC}}{{\sin {{87}^0}}}\\
\Rightarrow BC = \frac{{500\sin {{87}^0}}}{{\sin {{31}^0}}} = 969,5\left(m \right)\\
\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}} \Rightarrow \frac{{500}}{{\sin {{31}^0}}} = \frac{{AC}}{{\sin {{62}^0}}}\\
\Rightarrow AC = \frac{{500\sin {{62}^0}}}{{\sin {{31}^0}}} = 857,2\left(m \right)
\end{array}\)
- Tính C dựa vào công thức A+B+C=180
- Sử dụng định lí sin tính AC, BC:
\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}}\)
Lời giải chi tiết
Ta có \(\widehat {ACB} = {180^0} - \widehat {BAC} - \widehat {ABC}\) \(= {180^0} - {87^0} - {62^0} = {31^0}\)
Áp dụng định lí sin ta có
\(\begin{array}{l}
\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}} \Rightarrow \frac{{500}}{{\sin {{31}^0}}} = \frac{{BC}}{{\sin {{87}^0}}}\\
\Rightarrow BC = \frac{{500\sin {{87}^0}}}{{\sin {{31}^0}}} = 969,5\left(m \right)\\
\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}} \Rightarrow \frac{{500}}{{\sin {{31}^0}}} = \frac{{AC}}{{\sin {{62}^0}}}\\
\Rightarrow AC = \frac{{500\sin {{62}^0}}}{{\sin {{31}^0}}} = 857,2\left(m \right)
\end{array}\)