Câu hỏi: Cho tứ giác lồi ABCD có đường chéo \(AC = x\), đường chéo \(BD = y\) và góc tạo bởi \(AC\) và \(BD\) là \(\alpha \). Gọi \(S\) là diện tích của tứ giác \(ABCD\).
a) Chứng minh rằng \(S = \dfrac{1}{2}x. Y.\sin \alpha \).
b) Nêu kết quả trong trường hợp \(AC\) vuông góc với \(BD\).
a) Chứng minh rằng \(S = \dfrac{1}{2}x. Y.\sin \alpha \).
b) Nêu kết quả trong trường hợp \(AC\) vuông góc với \(BD\).
Phương pháp giải
a) Chia tứ giác thành hai tam giác và tính tổng diện tích hai tam giác này.
b) Dựa vào điều kiện \(AC \bot BD\) để suy ra góc giữa hai đường chéo và thay vào công thức đã có ở câu a.
Lời giải chi tiết
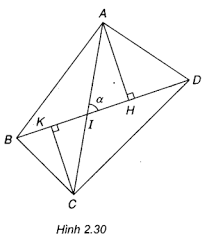
A) Ta có: \({S_{ABCD}} = {S_{ABD}} + {S_{CBD}}\)
Vẽ AH và CK vuông góc với BD.
Gọi I là giao điểm của hai đường chéo AC và BD.
Ta có: \(AH = AI\sin \alpha \), \(AK = CI\sin \alpha \)
\({S_{ABCD}} = \dfrac{1}{2}AH. BD + \dfrac{1}{2}CK. BD\)
\(= \dfrac{1}{2}BD\left( {AH + CK} \right)\)
\(= \dfrac{1}{2}BD\left( {AI + IC} \right)sin\alpha \)\(= \dfrac{1}{2}BD. AC\sin \alpha \)
Vậy \({S_{ABCD}} = \dfrac{1}{2}x. Y\sin \alpha \).
b) Nếu \(AC \bot BD\) thì \(\sin \alpha = 1\), khi đó \({S_{ABCD}} = \dfrac{1}{2}x. Y\).
Như vậy nếu tứ giác lồi ABCD có hai đường chéo AC và BD vuông góc với nhau thì diện tích của tứ giác bằng một nửa tích độ dài của hai đường chéo.
a) Chia tứ giác thành hai tam giác và tính tổng diện tích hai tam giác này.
b) Dựa vào điều kiện \(AC \bot BD\) để suy ra góc giữa hai đường chéo và thay vào công thức đã có ở câu a.
Lời giải chi tiết
A) Ta có: \({S_{ABCD}} = {S_{ABD}} + {S_{CBD}}\)
Vẽ AH và CK vuông góc với BD.
Gọi I là giao điểm của hai đường chéo AC và BD.
Ta có: \(AH = AI\sin \alpha \), \(AK = CI\sin \alpha \)
\({S_{ABCD}} = \dfrac{1}{2}AH. BD + \dfrac{1}{2}CK. BD\)
\(= \dfrac{1}{2}BD\left( {AH + CK} \right)\)
\(= \dfrac{1}{2}BD\left( {AI + IC} \right)sin\alpha \)\(= \dfrac{1}{2}BD. AC\sin \alpha \)
Vậy \({S_{ABCD}} = \dfrac{1}{2}x. Y\sin \alpha \).
b) Nếu \(AC \bot BD\) thì \(\sin \alpha = 1\), khi đó \({S_{ABCD}} = \dfrac{1}{2}x. Y\).
Như vậy nếu tứ giác lồi ABCD có hai đường chéo AC và BD vuông góc với nhau thì diện tích của tứ giác bằng một nửa tích độ dài của hai đường chéo.