Câu hỏi: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = {2^{|x|}}\) trên đoạn \(\displaystyle \left[ { - 1; 1} \right]\) .
Phương pháp giải
- Viết hàm số \(y = {2^{\left| x \right|}}\) dưới dạng khoảng.
- Xét từng hàm số có được trên các khoảng thích hợp.
- Tìm GTLN, GTNN và kết luận.
Lời giải chi tiết
Trên đoạn \(\displaystyle \left[ { - 1; 1} \right]\), ta có \(y = {2^{|x|}} = \left\{ {\begin{array}{*{20}{c}}{{2^x}, khi x \in {\rm{[}}0; 1]}\\{{2^{ - x}}, khi x \in {\rm{[}} - 1; 0]}\end{array}} \right.\)
+) Trên đoạn \(\displaystyle \left[ {0; 1} \right]\), hàm số \(y=2^x\) có \(2 > 1\) nên hàm đồng biến.
+) Trên đoạn \(\displaystyle \left[ { - 1; 0} \right]\) hàm số \(y=2^{-x} = \frac{1}{{{2^x}}} = {\left( {\frac{1}{2}} \right)^x}\) có \(0 < \frac{1}{2} < 1\) nên hàm nghịch biến.
+) Lại có \(y( - 1) = {2^{ - (- 1)}} = {2^1} = 2,\)\(y(0) = {2^0} = 1, y(1) = {2^1} = 2\).
BBT:
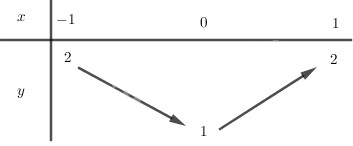
Vậy \(\mathop {\max }\limits_{{\rm{[}} - 1; 1]} y = y(1) = y(- 1) = 2,\)\(\mathop {\min }\limits_{{\rm{[}} - 1; 1]} y = y(0) = 1\).
- Viết hàm số \(y = {2^{\left| x \right|}}\) dưới dạng khoảng.
- Xét từng hàm số có được trên các khoảng thích hợp.
- Tìm GTLN, GTNN và kết luận.
Lời giải chi tiết
Trên đoạn \(\displaystyle \left[ { - 1; 1} \right]\), ta có \(y = {2^{|x|}} = \left\{ {\begin{array}{*{20}{c}}{{2^x}, khi x \in {\rm{[}}0; 1]}\\{{2^{ - x}}, khi x \in {\rm{[}} - 1; 0]}\end{array}} \right.\)
+) Trên đoạn \(\displaystyle \left[ {0; 1} \right]\), hàm số \(y=2^x\) có \(2 > 1\) nên hàm đồng biến.
+) Trên đoạn \(\displaystyle \left[ { - 1; 0} \right]\) hàm số \(y=2^{-x} = \frac{1}{{{2^x}}} = {\left( {\frac{1}{2}} \right)^x}\) có \(0 < \frac{1}{2} < 1\) nên hàm nghịch biến.
+) Lại có \(y( - 1) = {2^{ - (- 1)}} = {2^1} = 2,\)\(y(0) = {2^0} = 1, y(1) = {2^1} = 2\).
BBT:
Vậy \(\mathop {\max }\limits_{{\rm{[}} - 1; 1]} y = y(1) = y(- 1) = 2,\)\(\mathop {\min }\limits_{{\rm{[}} - 1; 1]} y = y(0) = 1\).