Câu hỏi: Cho hình chóp tứ giác đều \(S. ABCD\) có cạnh đáy bằng \(a\) và khoảng cách từ \(A\) đến mặt phẳng \(\left( {SBC} \right)\) bằng \(\dfrac{{a\sqrt 6 }}{3}\). Thể tích của hình chóp bằng:
A. \(\dfrac{{\sqrt 2 {a^3}}}{{16}}\)
B. \(\dfrac{{\sqrt 2 {a^3}}}{9}\)
C. \(\dfrac{{\sqrt 2 {a^3}}}{8}\)
D. \(\dfrac{{\sqrt 2 {a^3}}}{6}\)
A. \(\dfrac{{\sqrt 2 {a^3}}}{{16}}\)
B. \(\dfrac{{\sqrt 2 {a^3}}}{9}\)
C. \(\dfrac{{\sqrt 2 {a^3}}}{8}\)
D. \(\dfrac{{\sqrt 2 {a^3}}}{6}\)
Phương pháp giải
- Sử dụng tính chất \(d\left( {A,\left( {SBC} \right)} \right) = 2d\left({O,\left( {SBC} \right)} \right)\), từ đó xác định khoảng cách từ \(O\) đến \(\left( {SBC} \right)\).
- Tính chiều cao và diện tích đáy hình chóp.
- Tính thể tích theo công thức \(V = \dfrac{1}{3}Sh\).
Lời giải chi tiết
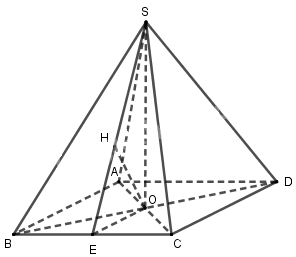
Gọi \(O\) là tâm đáy, \(E\) là trung điểm của \(BC\) và \(H\) là hình chiếu của \(O\) trên \(SE\).
Dễ thấy \(d\left( {A,\left( {SBC} \right)} \right) = 2d\left({O,\left( {SBC} \right)} \right)\) (vì \(AC = 2OC\)) nên \(d\left( {O,\left( {SBC} \right)} \right) = \dfrac{{a\sqrt 6 }}{6}\).
Lại có \(BC \bot \left( {SOE} \right) \Rightarrow BC \bot OH\), mà \(OH \bot SE\) nên \(OH \bot \left( {SBC} \right)\).
Do đó \(d\left( {O,\left( {SBC} \right)} \right) = OH = \dfrac{{a\sqrt 6 }}{6}\).
Tam giác \(SOE\) vuông tại \(O\) có \(OE = \dfrac{a}{2}, OH = \dfrac{{a\sqrt 6 }}{6}\) nên:
\(\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{E^2}}} + \dfrac{1}{{S{O^2}}}\) \(\Rightarrow SO = \dfrac{{OE. OH}}{{\sqrt {O{E^2} - O{H^2}} }}\) \(= \dfrac{{\dfrac{a}{2}.\dfrac{{a\sqrt 6 }}{6}}}{{\sqrt {\dfrac{{{a^2}}}{4} - \dfrac{{6{a^2}}}{{36}}} }} = \dfrac{{a\sqrt 2 }}{2}\)
Thể tích khối chóp \(V = \dfrac{1}{3}SO.{S_{ABCD}}\) \(= \dfrac{1}{3}.\dfrac{{a\sqrt 2 }}{2}.{a^2} = \dfrac{{{a^3}\sqrt 2 }}{6}\).
- Sử dụng tính chất \(d\left( {A,\left( {SBC} \right)} \right) = 2d\left({O,\left( {SBC} \right)} \right)\), từ đó xác định khoảng cách từ \(O\) đến \(\left( {SBC} \right)\).
- Tính chiều cao và diện tích đáy hình chóp.
- Tính thể tích theo công thức \(V = \dfrac{1}{3}Sh\).
Lời giải chi tiết
Gọi \(O\) là tâm đáy, \(E\) là trung điểm của \(BC\) và \(H\) là hình chiếu của \(O\) trên \(SE\).
Dễ thấy \(d\left( {A,\left( {SBC} \right)} \right) = 2d\left({O,\left( {SBC} \right)} \right)\) (vì \(AC = 2OC\)) nên \(d\left( {O,\left( {SBC} \right)} \right) = \dfrac{{a\sqrt 6 }}{6}\).
Lại có \(BC \bot \left( {SOE} \right) \Rightarrow BC \bot OH\), mà \(OH \bot SE\) nên \(OH \bot \left( {SBC} \right)\).
Do đó \(d\left( {O,\left( {SBC} \right)} \right) = OH = \dfrac{{a\sqrt 6 }}{6}\).
Tam giác \(SOE\) vuông tại \(O\) có \(OE = \dfrac{a}{2}, OH = \dfrac{{a\sqrt 6 }}{6}\) nên:
\(\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{E^2}}} + \dfrac{1}{{S{O^2}}}\) \(\Rightarrow SO = \dfrac{{OE. OH}}{{\sqrt {O{E^2} - O{H^2}} }}\) \(= \dfrac{{\dfrac{a}{2}.\dfrac{{a\sqrt 6 }}{6}}}{{\sqrt {\dfrac{{{a^2}}}{4} - \dfrac{{6{a^2}}}{{36}}} }} = \dfrac{{a\sqrt 2 }}{2}\)
Thể tích khối chóp \(V = \dfrac{1}{3}SO.{S_{ABCD}}\) \(= \dfrac{1}{3}.\dfrac{{a\sqrt 2 }}{2}.{a^2} = \dfrac{{{a^3}\sqrt 2 }}{6}\).
Đáp án D.