Câu hỏi: Cho hình lăng trụ \(ABC. A'B'C'\) có đáy là tam giác đều cạnh bằng \(a\), hình chiếu vuông góc của \(A'\) lên đáy \(\left( {ABC} \right)\) trùng với trọng tâm của tam giác \(ABC\) và cạnh bên tạo với đáy một góc \({60^0}\). Thể tích của hình lăng trụ là:
A. \(\dfrac{{\sqrt 3 }}{{12}}{a^3}\)
B. \(\dfrac{{\sqrt 3 }}{8}{a^3}\)
C. \(\dfrac{{\sqrt 3 }}{4}{a^3}\)
D. \(\dfrac{{\sqrt 3 }}{2}{a^3}\)
A. \(\dfrac{{\sqrt 3 }}{{12}}{a^3}\)
B. \(\dfrac{{\sqrt 3 }}{8}{a^3}\)
C. \(\dfrac{{\sqrt 3 }}{4}{a^3}\)
D. \(\dfrac{{\sqrt 3 }}{2}{a^3}\)
Phương pháp giải
- Xác định góc giữa cạnh bên và đáy (bằng góc giữa cạnh bên với hình chiếu của nó trên đáy).
- Tính diện tích tam giác đáy và chiều cao.
- Tính thể tích theo công thức \(V = Bh\).
Lời giải chi tiết
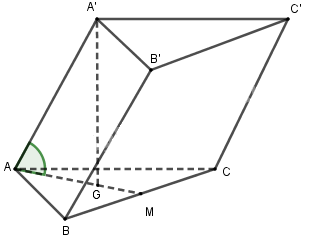
Gọi \(M\) là trung điểm của \(BC\) và \(G\) là trọng tâm tam giác \(ABC\).
Khi đó \(A'G \bot \left( {ABC} \right)\) và góc giữa \(A'A\) và \(\left( {ABC} \right)\) là \(\widehat {A'AG} = {60^0}\).
Tam giác \(ABC\) đều cạnh \(a\) nên \({S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\) và \(AG = \dfrac{2}{3}AM = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\).
Tam giác \(A'AG\) vuông tại \(G\) có \(AG = \dfrac{{a\sqrt 3 }}{3}\) và \(\widehat {A'AG} = {60^0}\) nên \(A'G = AG\tan {60^0} = a\).
Vậy thể tích \({V_{ABC. A'B'C'}} = {S_{ABC}}. A'G = \dfrac{{{a^2}\sqrt 3 }}{4}. A = \dfrac{{{a^3}\sqrt 3 }}{4}\).
- Xác định góc giữa cạnh bên và đáy (bằng góc giữa cạnh bên với hình chiếu của nó trên đáy).
- Tính diện tích tam giác đáy và chiều cao.
- Tính thể tích theo công thức \(V = Bh\).
Lời giải chi tiết
Gọi \(M\) là trung điểm của \(BC\) và \(G\) là trọng tâm tam giác \(ABC\).
Khi đó \(A'G \bot \left( {ABC} \right)\) và góc giữa \(A'A\) và \(\left( {ABC} \right)\) là \(\widehat {A'AG} = {60^0}\).
Tam giác \(ABC\) đều cạnh \(a\) nên \({S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\) và \(AG = \dfrac{2}{3}AM = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\).
Tam giác \(A'AG\) vuông tại \(G\) có \(AG = \dfrac{{a\sqrt 3 }}{3}\) và \(\widehat {A'AG} = {60^0}\) nên \(A'G = AG\tan {60^0} = a\).
Vậy thể tích \({V_{ABC. A'B'C'}} = {S_{ABC}}. A'G = \dfrac{{{a^2}\sqrt 3 }}{4}. A = \dfrac{{{a^3}\sqrt 3 }}{4}\).
Đáp án C.