Google
Câu hỏi: Cho hình chóp tứ giác đều $S.ABCD$ có đáy là hình vuông cạnh $a,$ cạnh bên $SA=\sqrt{2}a.$ Khoảng cách giữa hai đường thẳng chéo nhau $AB$ và $SC$ bằng
A. $\dfrac{\sqrt{42}a}{7}.$
B. $\dfrac{\sqrt{42}a}{14}.$
C. $\dfrac{2\sqrt{21}a}{7}.$
D. $\dfrac{\sqrt{21}a}{7}.$
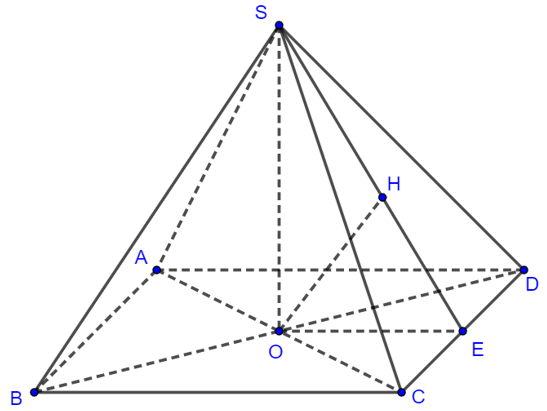Gọi $O$ là giao điểm của $AC$ và $BD$ thì $SO\bot \left( ABCD \right)$
Ta có: $d\left( AB,SC \right)=d\left( AB,\left( SCD \right) \right)=d\left( A,\left( SCD \right) \right)=2d\left( O,\left( SCD \right) \right)$
Hạ $OE\bot CD$, vì $\left\{ \begin{aligned}
& OH\bot SE \\
& OH\bot CD \\
\end{aligned} \right.\Rightarrow OH\bot \left( SCD \right)\Rightarrow d\left( O,\left( SCD \right) \right)=OH$
Hạ $OH\bot SE$ thì: $\left\{ \begin{aligned}
& OH\bot SE \\
& OH\bot CD \\
\end{aligned} \right.\Rightarrow OH\bot \left( SCD \right)$
Áp dụng định lí py – ta – go: $SO=\sqrt{S{{A}^{2}}-O{{A}^{2}}}=\dfrac{a\sqrt{6}}{2}$
Xét tam giác $SOE$ vuông tại $O$ ta có: $\dfrac{1}{O{{H}^{2}}}=\dfrac{1}{S{{O}^{2}}}+\dfrac{1}{O{{E}^{2}}}\Rightarrow OH=\dfrac{a\sqrt{42}}{14}$
$\Rightarrow d\left( AB,SC \right)=2OH=\dfrac{a\sqrt{42}}{7}.$
A. $\dfrac{\sqrt{42}a}{7}.$
B. $\dfrac{\sqrt{42}a}{14}.$
C. $\dfrac{2\sqrt{21}a}{7}.$
D. $\dfrac{\sqrt{21}a}{7}.$
Ta có: $d\left( AB,SC \right)=d\left( AB,\left( SCD \right) \right)=d\left( A,\left( SCD \right) \right)=2d\left( O,\left( SCD \right) \right)$
Hạ $OE\bot CD$, vì $\left\{ \begin{aligned}
& OH\bot SE \\
& OH\bot CD \\
\end{aligned} \right.\Rightarrow OH\bot \left( SCD \right)\Rightarrow d\left( O,\left( SCD \right) \right)=OH$
Hạ $OH\bot SE$ thì: $\left\{ \begin{aligned}
& OH\bot SE \\
& OH\bot CD \\
\end{aligned} \right.\Rightarrow OH\bot \left( SCD \right)$
Áp dụng định lí py – ta – go: $SO=\sqrt{S{{A}^{2}}-O{{A}^{2}}}=\dfrac{a\sqrt{6}}{2}$
Xét tam giác $SOE$ vuông tại $O$ ta có: $\dfrac{1}{O{{H}^{2}}}=\dfrac{1}{S{{O}^{2}}}+\dfrac{1}{O{{E}^{2}}}\Rightarrow OH=\dfrac{a\sqrt{42}}{14}$
$\Rightarrow d\left( AB,SC \right)=2OH=\dfrac{a\sqrt{42}}{7}.$
Đáp án A.
