Google
Câu hỏi: Cho hình chóp tứ giác $S.ABCD$ có đáy là hình thoi cạnh $2a$, $\widehat{ADC}={{60}^{0}}$, $SA\bot \left( ABCD \right)$ và góc hợp bởi $SC$ và đáy bằng ${{60}^{0}}$, $G$ là trọng tâm tam giác $SAC$. Khoảng cách từ điểm $G$ đến mặt phẳng $\left( SCD \right)$ bằng
A. $\dfrac{\sqrt{12}a}{\sqrt{15}}$.
B. $\dfrac{2a}{\sqrt{15}}$.
C. $\dfrac{\sqrt{3}a}{3}$.
D. $\dfrac{\sqrt{3}a}{2}$.
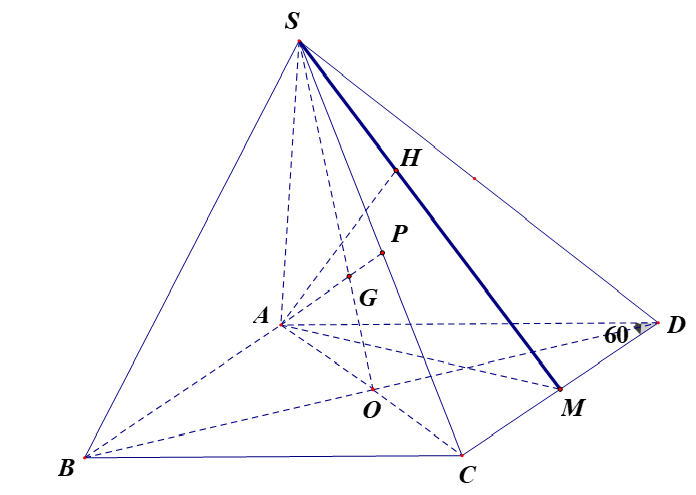Gọi $P$ là trung điểm của $SC$.
Ta có $\dfrac{d\left( G , \left( SCD \right) \right)}{d\left( A , \left( SCD \right) \right)}=\dfrac{PG}{PA}=\dfrac{1}{3}\Rightarrow d\left( G , \left( SCD \right) \right)=\dfrac{1}{3}d\left( A , \left( SCD \right) \right)$.
Gọi $M$ là trung điểm của cạnh $CD$.
Xét $\Delta ACD$, ta có $DA=DC=2a, \widehat{ADC}={{60}^{0}}$ nên $\Delta ACD$ đều do đó $AM\bot CD$.
Lại có $CD\bot SA \left( do SA \bot \left( ABCD \right) \right)$.
Từ đó suy ra $CD\bot \left( SAM \right)\Rightarrow \left( SCD \right)\bot \left( SAM \right)$.
Kẻ $AH\bot SM, H\in SM$.
Ta có $\left\{ \begin{aligned}
& \left( SCD \right)\bot \left( SAM \right) \\
& \left( SCD \right)\cap \left( SAM \right)=SM \\
& AH\bot SM \\
& AH\subset \left( SAM \right) \\
\end{aligned} \right.\Rightarrow AH\bot \left( SCD \right)\Rightarrow d\left( A,\left( SCD \right) \right)=AH$.
Lại có $\widehat{\left( SC, \left( ABCD \right) \right)}=\widehat{SCA}={{60}^{0}}\Rightarrow SA=AC.\tan {{60}^{0}}=2a\sqrt{3}$.
$\Delta ACD$ đều, suy ra $AM=\dfrac{2a\sqrt{3}}{2}=a\sqrt{3}$.
Trong tam giác vuông $SAM$, ta có: $\dfrac{1}{A{{H}^{2}}}=\dfrac{1}{{{\left( a\sqrt{3} \right)}^{2}}}+\dfrac{1}{{{\left( 2a\sqrt{3} \right)}^{2}}}=\dfrac{5}{12{{a}^{2}}}\Rightarrow AH=\dfrac{2a\sqrt{3}}{\sqrt{5}}$.
Vậy $d\left( G , \left( SCD \right) \right)=\dfrac{1}{3}AH=\dfrac{1}{3}.\dfrac{2a\sqrt{3}}{\sqrt{5}}=\dfrac{2a}{\sqrt{15}}$.
A. $\dfrac{\sqrt{12}a}{\sqrt{15}}$.
B. $\dfrac{2a}{\sqrt{15}}$.
C. $\dfrac{\sqrt{3}a}{3}$.
D. $\dfrac{\sqrt{3}a}{2}$.
Ta có $\dfrac{d\left( G , \left( SCD \right) \right)}{d\left( A , \left( SCD \right) \right)}=\dfrac{PG}{PA}=\dfrac{1}{3}\Rightarrow d\left( G , \left( SCD \right) \right)=\dfrac{1}{3}d\left( A , \left( SCD \right) \right)$.
Gọi $M$ là trung điểm của cạnh $CD$.
Xét $\Delta ACD$, ta có $DA=DC=2a, \widehat{ADC}={{60}^{0}}$ nên $\Delta ACD$ đều do đó $AM\bot CD$.
Lại có $CD\bot SA \left( do SA \bot \left( ABCD \right) \right)$.
Từ đó suy ra $CD\bot \left( SAM \right)\Rightarrow \left( SCD \right)\bot \left( SAM \right)$.
Kẻ $AH\bot SM, H\in SM$.
Ta có $\left\{ \begin{aligned}
& \left( SCD \right)\bot \left( SAM \right) \\
& \left( SCD \right)\cap \left( SAM \right)=SM \\
& AH\bot SM \\
& AH\subset \left( SAM \right) \\
\end{aligned} \right.\Rightarrow AH\bot \left( SCD \right)\Rightarrow d\left( A,\left( SCD \right) \right)=AH$.
Lại có $\widehat{\left( SC, \left( ABCD \right) \right)}=\widehat{SCA}={{60}^{0}}\Rightarrow SA=AC.\tan {{60}^{0}}=2a\sqrt{3}$.
$\Delta ACD$ đều, suy ra $AM=\dfrac{2a\sqrt{3}}{2}=a\sqrt{3}$.
Trong tam giác vuông $SAM$, ta có: $\dfrac{1}{A{{H}^{2}}}=\dfrac{1}{{{\left( a\sqrt{3} \right)}^{2}}}+\dfrac{1}{{{\left( 2a\sqrt{3} \right)}^{2}}}=\dfrac{5}{12{{a}^{2}}}\Rightarrow AH=\dfrac{2a\sqrt{3}}{\sqrt{5}}$.
Vậy $d\left( G , \left( SCD \right) \right)=\dfrac{1}{3}AH=\dfrac{1}{3}.\dfrac{2a\sqrt{3}}{\sqrt{5}}=\dfrac{2a}{\sqrt{15}}$.
Đáp án B.