Câu hỏi: Cho tứ giác \(ABCD\). Các điểm \(M, N , P\) và \(Q\) lần lượt là trung điểm của \(AB, BC, CD\) và \(DA\). Chứng minh rằng hai tam giác \(ANP\) và \(CMQ\) có cùng trọng tâm.
Phương pháp giải
- Gọi \(G\) là trọng tâm của tam giác \(ANP\).
- Chứng minh \(\overrightarrow {GC} + \overrightarrow {GM} + \overrightarrow {GQ} = \overrightarrow 0 \) và kết luận.
Lời giải chi tiết
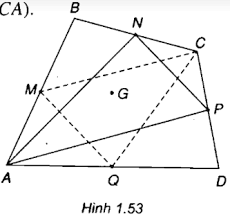
Gọi \(G \) là trọng tâm của tam giác \(ANP\).
Khi đó \(\overrightarrow {GA} + \overrightarrow {GN} + \overrightarrow {GP} = \overrightarrow 0 \)
Ta có: \(\overrightarrow {GC} + \overrightarrow {GM} + \overrightarrow {GQ} \)\(= \overrightarrow {GA} + \overrightarrow {AC} + \overrightarrow {GN} \) \(+ \overrightarrow {NM} + \overrightarrow {GP} + \overrightarrow {PQ} \) \(= (\overrightarrow {GA} + \overrightarrow {GN} + \overrightarrow {GP}) + \overrightarrow {AC} + (\overrightarrow {NM} + \overrightarrow {PQ})\)
\(= \overrightarrow {AC} + \overrightarrow {CA} = \overrightarrow 0 \)
(Vì \(\overrightarrow {NM} = \dfrac{1}{2}\overrightarrow {CA} ,\overrightarrow {PQ} = \dfrac{1}{2}\overrightarrow {CA} \) nên \(\overrightarrow {NM} + \overrightarrow {PQ} = \overrightarrow {CA} \)).
Vậy \(\overrightarrow {GC} + \overrightarrow {GM} + \overrightarrow {GQ} = \overrightarrow 0 \)
Suy ra \(G\) là trọng tâm của tam giác \(CMQ\).
- Gọi \(G\) là trọng tâm của tam giác \(ANP\).
- Chứng minh \(\overrightarrow {GC} + \overrightarrow {GM} + \overrightarrow {GQ} = \overrightarrow 0 \) và kết luận.
Lời giải chi tiết
Gọi \(G \) là trọng tâm của tam giác \(ANP\).
Khi đó \(\overrightarrow {GA} + \overrightarrow {GN} + \overrightarrow {GP} = \overrightarrow 0 \)
Ta có: \(\overrightarrow {GC} + \overrightarrow {GM} + \overrightarrow {GQ} \)\(= \overrightarrow {GA} + \overrightarrow {AC} + \overrightarrow {GN} \) \(+ \overrightarrow {NM} + \overrightarrow {GP} + \overrightarrow {PQ} \) \(= (\overrightarrow {GA} + \overrightarrow {GN} + \overrightarrow {GP}) + \overrightarrow {AC} + (\overrightarrow {NM} + \overrightarrow {PQ})\)
\(= \overrightarrow {AC} + \overrightarrow {CA} = \overrightarrow 0 \)
(Vì \(\overrightarrow {NM} = \dfrac{1}{2}\overrightarrow {CA} ,\overrightarrow {PQ} = \dfrac{1}{2}\overrightarrow {CA} \) nên \(\overrightarrow {NM} + \overrightarrow {PQ} = \overrightarrow {CA} \)).
Vậy \(\overrightarrow {GC} + \overrightarrow {GM} + \overrightarrow {GQ} = \overrightarrow 0 \)
Suy ra \(G\) là trọng tâm của tam giác \(CMQ\).