Câu hỏi: Trong mặt phẳng tọa độ Oxy, cho elip (E) : \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\left( {a > b > 1} \right).\) Một góc vuông \(uOv\) (vuông tại O) quay quanh gốc O, cắt elip (E) tại M và N. Chứng minh rằng \(\frac{1}{{O{M^2}}} + \frac{1}{{O{N^2}}}\) không đổi, từ đó suy ra MN luôn tiếp xúc với một đường tròn cố định.
Lời giải chi tiết
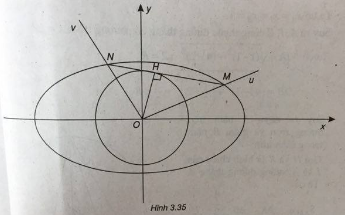
Gọi \(y = kx\) và \(y = - \frac{1}{k}x\) là phương trình của \(Ou\) và \(Ov\).
Phương trình hoành độ giao điểm của \(Ou\) và elip (E)
\(\frac{{{x^2}}}{{{a^2}}} + \frac{{{k^2}{x^2}}}{{{b^2}}} = 1 \Leftrightarrow x_M^2 = \frac{{{a^2}{b^2}}}{{{b^2} + {k^2}{a^2}}}.\)
Ta có : \(O{M^2} = x_M^2 + y_M^2 = x_M^2 + {k^2}x_M^2\) \(= x_M^2({k^2} + 1) = \frac{{{a^2}{b^2}(1 + {k^2})}}{{{b^2} + {k^2}{a^2}}}\).
…………
Suy ra : \(\frac{1}{{O{M^2}}} = \frac{{{b^2} + {k^2}{a^2}}}{{{a^2}{b^2}(1 + {k^2})}}.\)
Tương tự \(\frac{1}{{O{N^2}}} = \frac{{{b^2} + \frac{1}{{{k^2}}}{a^2}}}{{{a^2}{b^2}\left( {1 + \frac{1}{{{k^2}}}} \right)}} = \frac{{{a^2} + {k^2}{b^2}}}{{{a^2}{b^2}(1 + {k^2})}}.\)
Suy ra \(\frac{1}{{O{M^2}}} + \frac{1}{{O{N^2}}} = \frac{{{a^2} + {b^2} + {k^2}\left( {{a^2} + {b^2}} \right)}}{{{a^2}{b^2}\left({1 + {k^2}} \right)}} = \frac{{{a^2} + {b^2}}}{{{a^2}{b^2}}}.\)
Vậy \(\frac{1}{{O{M^2}}} + \frac{1}{{O{N^2}}}\) không đổi.
Vẽ đường cao OH của tam giác vuông OMN.
Ta có : \(\frac{1}{{O{H^2}}} = \frac{1}{{O{M^2}}} + \frac{1}{{O{N^2}}} = \frac{{{a^2} + {b^2}}}{{{a^2}{b^2}}}.\)
Suy ra \(OH = \frac{{ab}}{{\sqrt {{a^2} + {b^2}} }} = R\) không đổi.
Vậy MN luôn tiếp xúc với đường tròn cố định tâ O bán kính \(R = \frac{{ab}}{{\sqrt {{a^2} + {b^2}} }}.\)
Gọi \(y = kx\) và \(y = - \frac{1}{k}x\) là phương trình của \(Ou\) và \(Ov\).
Phương trình hoành độ giao điểm của \(Ou\) và elip (E)
\(\frac{{{x^2}}}{{{a^2}}} + \frac{{{k^2}{x^2}}}{{{b^2}}} = 1 \Leftrightarrow x_M^2 = \frac{{{a^2}{b^2}}}{{{b^2} + {k^2}{a^2}}}.\)
Ta có : \(O{M^2} = x_M^2 + y_M^2 = x_M^2 + {k^2}x_M^2\) \(= x_M^2({k^2} + 1) = \frac{{{a^2}{b^2}(1 + {k^2})}}{{{b^2} + {k^2}{a^2}}}\).
…………
Suy ra : \(\frac{1}{{O{M^2}}} = \frac{{{b^2} + {k^2}{a^2}}}{{{a^2}{b^2}(1 + {k^2})}}.\)
Tương tự \(\frac{1}{{O{N^2}}} = \frac{{{b^2} + \frac{1}{{{k^2}}}{a^2}}}{{{a^2}{b^2}\left( {1 + \frac{1}{{{k^2}}}} \right)}} = \frac{{{a^2} + {k^2}{b^2}}}{{{a^2}{b^2}(1 + {k^2})}}.\)
Suy ra \(\frac{1}{{O{M^2}}} + \frac{1}{{O{N^2}}} = \frac{{{a^2} + {b^2} + {k^2}\left( {{a^2} + {b^2}} \right)}}{{{a^2}{b^2}\left({1 + {k^2}} \right)}} = \frac{{{a^2} + {b^2}}}{{{a^2}{b^2}}}.\)
Vậy \(\frac{1}{{O{M^2}}} + \frac{1}{{O{N^2}}}\) không đổi.
Vẽ đường cao OH của tam giác vuông OMN.
Ta có : \(\frac{1}{{O{H^2}}} = \frac{1}{{O{M^2}}} + \frac{1}{{O{N^2}}} = \frac{{{a^2} + {b^2}}}{{{a^2}{b^2}}}.\)
Suy ra \(OH = \frac{{ab}}{{\sqrt {{a^2} + {b^2}} }} = R\) không đổi.
Vậy MN luôn tiếp xúc với đường tròn cố định tâ O bán kính \(R = \frac{{ab}}{{\sqrt {{a^2} + {b^2}} }}.\)