Câu hỏi: Cho tam giác đều \(ABC\) có \(O\) là trọng tâm và \(M\) là một điểm tùy ý trong tam giác. Gọi \(D, E, F\) lần lượt là chân đường vuông góc hạ từ \(M\) đến \(BC, AC, AB\). Chứng minh rằng: \(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \dfrac{3}{2}\overrightarrow {MO} \).
Phương pháp giải
- Qua \(M \) kẻ các đường thẳng \({K_1}{K_4}//AB\), \({K_2}{K_5}//AC\), \({K_3}{K_6}//BC\).
- Tính tổng các véc tơ \(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} \), sử dụng quy tắc hình bình hành và kết luận.
Lời giải chi tiết
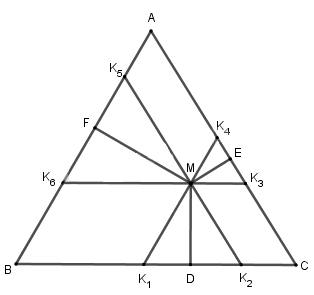
Qua \(M \) kẻ các đường thẳng sau: \({K_1}{K_4}//AB\), \({K_2}{K_5}//AC\), \({K_3}{K_6}//BC\)
(\({K_1},{K_2} \in BC;{K_3},{K_4} \in AC;{K_5},{K_6} \in AB\)). Ta có:
$\overrightarrow{M D}+\overrightarrow{M E}+\overrightarrow{M F}=\frac{1}{2}\left(\overline{M K_{1}}+\overline{M K_{2}}\right)+\frac{1}{2}\left(\overline{M K_{3}}+\overline{M K_{4}}\right)+\frac{1}{2}\left(\overline{M K_{5}}+\overline{M K_{6}}\right)$
$=\frac{1}{2}\left(\overline{M K_{1}}+\overline{M K_{2}}+\overline{M K_{3}}+\overline{M K_{4}}+\overline{M K_{5}}+\overline{M K_{6}}\right)$
$=\frac{1}{2}\left[\left(\overrightarrow{M K_{1}}+\overline{M K_{6}}\right)+\left(\overline{M K_{2}}+\overline{M K_{3}}\right)+\left(\overrightarrow{M K_{4}}+\overline{M K_{5}}\right)\right]$
$=\frac{1}{2}[\overrightarrow{M A}+\overrightarrow{M B}+\overrightarrow{M C}]$
$=\frac{1}{2} \cdot 3 \overrightarrow{M O}=\frac{3}{2} \overrightarrow{M O}$
(Vì \(M{K_5}A{K_4}, M{K_3}C{K_2}, M{K_1}B{K_6}\) là các hình bình hành).
Vậy \(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \dfrac{3}{2}\overrightarrow {MO} \).
- Qua \(M \) kẻ các đường thẳng \({K_1}{K_4}//AB\), \({K_2}{K_5}//AC\), \({K_3}{K_6}//BC\).
- Tính tổng các véc tơ \(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} \), sử dụng quy tắc hình bình hành và kết luận.
Lời giải chi tiết
Qua \(M \) kẻ các đường thẳng sau: \({K_1}{K_4}//AB\), \({K_2}{K_5}//AC\), \({K_3}{K_6}//BC\)
(\({K_1},{K_2} \in BC;{K_3},{K_4} \in AC;{K_5},{K_6} \in AB\)). Ta có:
$\overrightarrow{M D}+\overrightarrow{M E}+\overrightarrow{M F}=\frac{1}{2}\left(\overline{M K_{1}}+\overline{M K_{2}}\right)+\frac{1}{2}\left(\overline{M K_{3}}+\overline{M K_{4}}\right)+\frac{1}{2}\left(\overline{M K_{5}}+\overline{M K_{6}}\right)$
$=\frac{1}{2}\left(\overline{M K_{1}}+\overline{M K_{2}}+\overline{M K_{3}}+\overline{M K_{4}}+\overline{M K_{5}}+\overline{M K_{6}}\right)$
$=\frac{1}{2}\left[\left(\overrightarrow{M K_{1}}+\overline{M K_{6}}\right)+\left(\overline{M K_{2}}+\overline{M K_{3}}\right)+\left(\overrightarrow{M K_{4}}+\overline{M K_{5}}\right)\right]$
$=\frac{1}{2}[\overrightarrow{M A}+\overrightarrow{M B}+\overrightarrow{M C}]$
$=\frac{1}{2} \cdot 3 \overrightarrow{M O}=\frac{3}{2} \overrightarrow{M O}$
(Vì \(M{K_5}A{K_4}, M{K_3}C{K_2}, M{K_1}B{K_6}\) là các hình bình hành).
Vậy \(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \dfrac{3}{2}\overrightarrow {MO} \).