Câu hỏi: Cho tam giác \(ABC\) đều có trọng tâm \(O.\) \(M\) là một điểm tùy ý nằm trong tam giác. Gọi \(D, E, F\) theo thứ tự là hình chiếu vuông góc của \(M\) trên \(BC, CA, AB.\) Chứng minh rằng \(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{3}{2}\overrightarrow {MO} .\)
Lời giải chi tiết
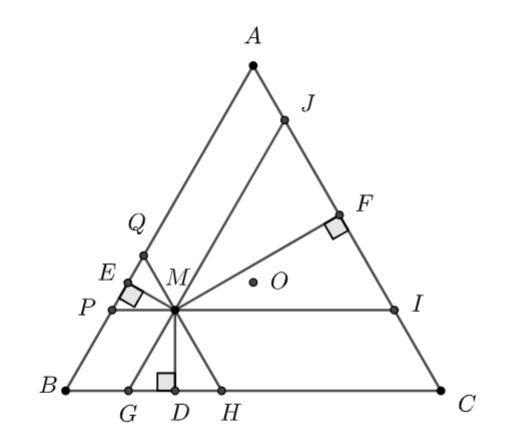
Gọi đường thẳng đi qua \(M\) và song song với \(AB\) cắt \(BC, AC\) lần lượt tại \(G, J\); đường thẳng đi qua \(M\) và song song với \(BC\) cắt \(AB, AC\) lần lượt tại \(P, I\); đường thẳng đi qua \(M\) và song song với \(AC\) cắt \(AB, BC\) lần lượt tại \(Q, H\).
Ta có: \(MG\)//\(AB\) \( \Rightarrow \) \(\widehat {MGH} = \widehat {ABC} = {60^ \circ }\)
\(MH\)//\(AC\) \( \Rightarrow \) \(\widehat {MHG} = \widehat {ACB} = {60^ \circ }\)
\( \Rightarrow \) \(\Delta MHG\) là tam giác đều
Mặt khác \(MD \bot HG\)
\( \Rightarrow \) \(D\) là trung điểm của \(GH\)
\( \Rightarrow \) \(2\overrightarrow {MD} = \overrightarrow {MG} + \overrightarrow {MH} \) (1)
Chứng minh tương tự ta được: \(2\overrightarrow {ME} = \overrightarrow {MQ} + \overrightarrow {MP} \), \(2\overrightarrow {MF} = \overrightarrow {MI} + \overrightarrow {MJ} \) (2)
Ta có: tứ giác \(AQMJ,\) \(BPMG,\) \(CIMH\) là hình bình hành
Từ (1) và (2) \( \Rightarrow \) \(2\left( {\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} } \right) = \overrightarrow {MG} + \overrightarrow {MH} + \overrightarrow {MQ} + \overrightarrow {MP} + \overrightarrow {MI} + \overrightarrow {MJ} \)
\(\begin{array}{l} = \left( {\overrightarrow {MG} + \overrightarrow {MJ} } \right) + \left( {\overrightarrow {MI} + \overrightarrow {MH} } \right) + \left( {\overrightarrow {MP} + \overrightarrow {MG} } \right)\\ = \overrightarrow {MA} + \overrightarrow {MC} + \overrightarrow {MB} \\ = \overrightarrow {MO} + \overrightarrow {OA} + \overrightarrow {MO} + \overrightarrow {OC} + \overrightarrow {MO} + \overrightarrow {OB} \\ = 3\overrightarrow {MO} + \left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right)\\ = 3\overrightarrow {MO} \end{array}\)
\( \Rightarrow \) \(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{3}{2}\overrightarrow {MO} \) (đpcm)
Gọi đường thẳng đi qua \(M\) và song song với \(AB\) cắt \(BC, AC\) lần lượt tại \(G, J\); đường thẳng đi qua \(M\) và song song với \(BC\) cắt \(AB, AC\) lần lượt tại \(P, I\); đường thẳng đi qua \(M\) và song song với \(AC\) cắt \(AB, BC\) lần lượt tại \(Q, H\).
Ta có: \(MG\)//\(AB\) \( \Rightarrow \) \(\widehat {MGH} = \widehat {ABC} = {60^ \circ }\)
\(MH\)//\(AC\) \( \Rightarrow \) \(\widehat {MHG} = \widehat {ACB} = {60^ \circ }\)
\( \Rightarrow \) \(\Delta MHG\) là tam giác đều
Mặt khác \(MD \bot HG\)
\( \Rightarrow \) \(D\) là trung điểm của \(GH\)
\( \Rightarrow \) \(2\overrightarrow {MD} = \overrightarrow {MG} + \overrightarrow {MH} \) (1)
Chứng minh tương tự ta được: \(2\overrightarrow {ME} = \overrightarrow {MQ} + \overrightarrow {MP} \), \(2\overrightarrow {MF} = \overrightarrow {MI} + \overrightarrow {MJ} \) (2)
Ta có: tứ giác \(AQMJ,\) \(BPMG,\) \(CIMH\) là hình bình hành
Từ (1) và (2) \( \Rightarrow \) \(2\left( {\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} } \right) = \overrightarrow {MG} + \overrightarrow {MH} + \overrightarrow {MQ} + \overrightarrow {MP} + \overrightarrow {MI} + \overrightarrow {MJ} \)
\(\begin{array}{l} = \left( {\overrightarrow {MG} + \overrightarrow {MJ} } \right) + \left( {\overrightarrow {MI} + \overrightarrow {MH} } \right) + \left( {\overrightarrow {MP} + \overrightarrow {MG} } \right)\\ = \overrightarrow {MA} + \overrightarrow {MC} + \overrightarrow {MB} \\ = \overrightarrow {MO} + \overrightarrow {OA} + \overrightarrow {MO} + \overrightarrow {OC} + \overrightarrow {MO} + \overrightarrow {OB} \\ = 3\overrightarrow {MO} + \left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right)\\ = 3\overrightarrow {MO} \end{array}\)
\( \Rightarrow \) \(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{3}{2}\overrightarrow {MO} \) (đpcm)