Câu hỏi: Cho nửa đường tròn tâm \(O\) đường kính \(AB.\) Gọi \(Ax, By\) là các tia vuông góc với \(AB\) \((Ax,By\) và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ \(AB).\) Gọi \(M\) là điểm bất kì thuộc tia \(Ax.\) Qua \(M\) kẻ tiếp tuyến với nửa đường tròn, cắt \(By\) ở \(N.\)
\(a)\) Tính số đo góc \(MON.\)
\(b)\) Chứng minh rằng \(MN = AM + BN.\)
\(c)\) Chứng minh rằng \(AM.BN = R^2\) \((R\) là bán kính của nửa đường tròn\().\)
\(a)\) Tính số đo góc \(MON.\)
\(b)\) Chứng minh rằng \(MN = AM + BN.\)
\(c)\) Chứng minh rằng \(AM.BN = R^2\) \((R\) là bán kính của nửa đường tròn\().\)
Phương pháp giải
Sử dụng kiến thức: Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì
+) Điểm đó cách đều hai tiếp điểm.
+) Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.
+) Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.
Sử dụng hệ thức lượng trong tam giác vuông: Trong tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.
Lời giải chi tiết
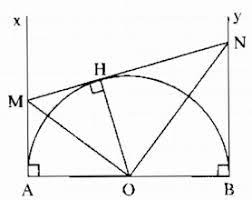
\(a)\) Gọi \(H\) là tiếp điểm của tiếp tuyến \(MN\) với đường tròn \((O).\) Nối \(OH.\)
Ta có: \(\widehat {AOH} + \widehat {BOH} = 180^\circ \) (hai góc kề bù)
\(OM\) là tia phân giác của góc \(AOH\) (tính chất hai tiếp tuyến cắt nhau)
\(ON\) là tia phân giác của góc \(BOH\) (tính chất hai tiếp tuyến cắt nhau)
Suy ra: \(OM ⊥ ON\) (tính chất hai góc kề bù)
Vậy \(\widehat {MON} = 90^\circ \)
\(b)\) Ta có: \(MA = MH\) (tính chất hai tiếp tuyến cắt nhau)
\(NB = NH\) (tính chất hai tiếp tuyến cắt nhau)
Mà: \(MN = MH + HN\)
Suy ra: \( MN = AM + BN\)
\(c)\) Tam giác \(OMN\) vuông tại \(O\) có \(OH ⊥ MN\) (tính chất tiếp tuyến), theo hệ thức lượng trong tam giác vuông, ta có:
\(O{H^2} = MH.NH\)
Mà: \( MH = MA, NH = NB\) (chứng minh trên)
Suy ra: \(AM.BN = O{H^2} = {R^2}\).
Sử dụng kiến thức: Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì
+) Điểm đó cách đều hai tiếp điểm.
+) Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.
+) Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.
Sử dụng hệ thức lượng trong tam giác vuông: Trong tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.
Lời giải chi tiết
\(a)\) Gọi \(H\) là tiếp điểm của tiếp tuyến \(MN\) với đường tròn \((O).\) Nối \(OH.\)
Ta có: \(\widehat {AOH} + \widehat {BOH} = 180^\circ \) (hai góc kề bù)
\(OM\) là tia phân giác của góc \(AOH\) (tính chất hai tiếp tuyến cắt nhau)
\(ON\) là tia phân giác của góc \(BOH\) (tính chất hai tiếp tuyến cắt nhau)
Suy ra: \(OM ⊥ ON\) (tính chất hai góc kề bù)
Vậy \(\widehat {MON} = 90^\circ \)
\(b)\) Ta có: \(MA = MH\) (tính chất hai tiếp tuyến cắt nhau)
\(NB = NH\) (tính chất hai tiếp tuyến cắt nhau)
Mà: \(MN = MH + HN\)
Suy ra: \( MN = AM + BN\)
\(c)\) Tam giác \(OMN\) vuông tại \(O\) có \(OH ⊥ MN\) (tính chất tiếp tuyến), theo hệ thức lượng trong tam giác vuông, ta có:
\(O{H^2} = MH.NH\)
Mà: \( MH = MA, NH = NB\) (chứng minh trên)
Suy ra: \(AM.BN = O{H^2} = {R^2}\).