Câu hỏi: Cho đường tròn \((O),\) điểm \(A\) nằm bên ngoài đường tròn. Kẻ các tiếp tuyến \(AM, AN\) với đường tròn \((M,N\) là các tiếp điểm\().\)
\(a)\) Chứng minh rằng \(OA ⊥ MN.\)
\(b)\) Vẽ đường kính \(NOC.\) Chứng minh rằng \(MC // AO.\)
\(c)\) Tính độ dài các cạnh của tam giác \(AMN\) biết \(OM = 3cm,\) \(OA = 5cm.\)
\(a)\) Chứng minh rằng \(OA ⊥ MN.\)
\(b)\) Vẽ đường kính \(NOC.\) Chứng minh rằng \(MC // AO.\)
\(c)\) Tính độ dài các cạnh của tam giác \(AMN\) biết \(OM = 3cm,\) \(OA = 5cm.\)
Phương pháp giải
Sử dụng kiến thức:
\(*\)) Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì
+) Điểm đó cách đều hai tiếp điểm.
+) Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.
\(*\)) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
Lời giải chi tiết
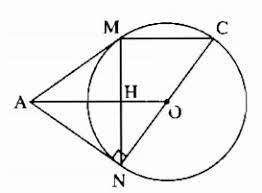
\(a)\) Xét đường tròn (O) có \(AM\) và \(AN\) là hai tiếp tuyến cắt nhau tại A nên \(AM = AN\) ( tính chất hai tiếp tuyến cắt nhau)
Suy ra tam giác \(AMN\) cân tại \(A\)
Mặt khác \(AO\) là đường phân giác của góc \(MAN\) ( tính chất hai tiếp tuyến cắt nhau)
Suy ra \(AO\) là đường cao của tam giác \(AMN\) (tính chất tam giác cân)
Vậy \(OA ⊥ MN.\)
\(b)\) Tam giác \(MNC\) nội tiếp trong đường tròn \((O)\) có \(NC\) là đường kính nên \(\widehat {CMN} = 90^\circ \)
suy ra: \(MN ⊥ MC\)
Mà \(OA ⊥ MN\) (chứng minh trên)
Suy ra: \(OA // MC\)
\(c)\) Ta có: \(AN ⊥ NC\) (tính chất tiếp tuyến)
Áp dụng định lí Pi-ta-go vào tam giác vuông \(AON\) ta có:
\(A{O^2} = A{N^2} + O{N^2}\)
Suy ra: \(A{N^2} = A{O^2} - O{N^2} = {5^2} - {3^2} = 16\)
\( AN = 4 (cm)\)
Suy ra: \(AM = AN = 4 (cm)\)
Gọi \(H\) là giao điểm của \(AO\) và \(MN\). Xét tam giác AMN cân tại A có AH là đường phân giác nên AH cũng là đường trung tuyến (tính chất tam giác cân).
Suy ra \(MH = NH = \displaystyle {{MN} \over 2}\)
Tam giác \(AON\) vuông tại \(N\) có \(NH ⊥ AO.\) Theo hệ thức lượng trong tam giác vuông, ta có:
\(OA.NH = AN.ON\)\( \Rightarrow NH = \displaystyle {{AN.ON} \over {AO}}\)\( = \displaystyle {{4.3} \over 5} = 2,4 (cm) \)
Từ đó: \(MN = 2.NH = 2.2,4 = 4,8 (cm).\)
Sử dụng kiến thức:
\(*\)) Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì
+) Điểm đó cách đều hai tiếp điểm.
+) Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.
\(*\)) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
Lời giải chi tiết
\(a)\) Xét đường tròn (O) có \(AM\) và \(AN\) là hai tiếp tuyến cắt nhau tại A nên \(AM = AN\) ( tính chất hai tiếp tuyến cắt nhau)
Suy ra tam giác \(AMN\) cân tại \(A\)
Mặt khác \(AO\) là đường phân giác của góc \(MAN\) ( tính chất hai tiếp tuyến cắt nhau)
Suy ra \(AO\) là đường cao của tam giác \(AMN\) (tính chất tam giác cân)
Vậy \(OA ⊥ MN.\)
\(b)\) Tam giác \(MNC\) nội tiếp trong đường tròn \((O)\) có \(NC\) là đường kính nên \(\widehat {CMN} = 90^\circ \)
suy ra: \(MN ⊥ MC\)
Mà \(OA ⊥ MN\) (chứng minh trên)
Suy ra: \(OA // MC\)
\(c)\) Ta có: \(AN ⊥ NC\) (tính chất tiếp tuyến)
Áp dụng định lí Pi-ta-go vào tam giác vuông \(AON\) ta có:
\(A{O^2} = A{N^2} + O{N^2}\)
Suy ra: \(A{N^2} = A{O^2} - O{N^2} = {5^2} - {3^2} = 16\)
\( AN = 4 (cm)\)
Suy ra: \(AM = AN = 4 (cm)\)
Gọi \(H\) là giao điểm của \(AO\) và \(MN\). Xét tam giác AMN cân tại A có AH là đường phân giác nên AH cũng là đường trung tuyến (tính chất tam giác cân).
Suy ra \(MH = NH = \displaystyle {{MN} \over 2}\)
Tam giác \(AON\) vuông tại \(N\) có \(NH ⊥ AO.\) Theo hệ thức lượng trong tam giác vuông, ta có:
\(OA.NH = AN.ON\)\( \Rightarrow NH = \displaystyle {{AN.ON} \over {AO}}\)\( = \displaystyle {{4.3} \over 5} = 2,4 (cm) \)
Từ đó: \(MN = 2.NH = 2.2,4 = 4,8 (cm).\)