Câu hỏi: Cho hai điểm \(A, B\) và đường tròn tâm \(O\) không có điểm chung với đường thẳng \(AB\). Qua mỗi điểm \(M\) chạy trên đường tròn \((O)\) dựng hình bình hành \(MABN\). Chứng mình rằng điểm \(N\) thuộc một đường tròn xác định.
Phương pháp giải
Chứng minh điểm N là ảnh của điểm N qua 1 phép tịnh tiến theo vector cố định, sử dụng tính chất ảnh của 1 đường tròn qua một phép tịnh tiến là đường tròn bằng nó.
Lời giải chi tiết
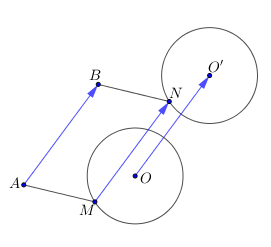
Vì \(MABN\) là hình bình hành nên \(\vec{MN}=\vec{AB}\) không đổi.
\(\Rightarrow {T_{\overrightarrow {AB} }}\left( M \right) = N\).
Ta có ảnh của 1 đường tròn qua một phép tịnh tiến là đường tròn bằng nó nên khi \(M\) chạy trên đường tròn \((O)\) thì \(N\) chạy trên đường tròn \((O')\) là ảnh của \((O)\) qua phép tịnh tiến theo \(\vec{AB}\), đường tròn này là xác định (đpcm).
Chứng minh điểm N là ảnh của điểm N qua 1 phép tịnh tiến theo vector cố định, sử dụng tính chất ảnh của 1 đường tròn qua một phép tịnh tiến là đường tròn bằng nó.
Lời giải chi tiết
Vì \(MABN\) là hình bình hành nên \(\vec{MN}=\vec{AB}\) không đổi.
\(\Rightarrow {T_{\overrightarrow {AB} }}\left( M \right) = N\).
Ta có ảnh của 1 đường tròn qua một phép tịnh tiến là đường tròn bằng nó nên khi \(M\) chạy trên đường tròn \((O)\) thì \(N\) chạy trên đường tròn \((O')\) là ảnh của \((O)\) qua phép tịnh tiến theo \(\vec{AB}\), đường tròn này là xác định (đpcm).