Câu hỏi: Với số \(α, 0 < \alpha < {\pi \over 2}\), xét điểm M của đường tròn lượng giác xác định bởi 2α, rồi xét tam giác vuông A’MA (A’ đối xứng với A qua tâm O của đường tròn).
Lời giải chi tiết:
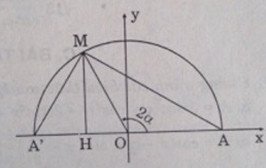
Ta có:
\(\eqalign{
& A{M^2} = \overline {AH} .\overline {{\rm{AA}}} {\rm{' = (}}\overline {AO} + \overline {OH}).\overline {{\rm{AA}}'} \cr
& = (- 1 + \cos 2\alpha)(- 2) = 2(1 - \cos 2\alpha) \cr} \)
Lại có:
\(\begin{array}{l}
\left\{ \begin{array}{l}
2\alpha = \widehat {AOM} = \widehat {OA'M} + \widehat {OMA'}\\
\widehat {OA'M} = \widehat {OMA'}\left({\Delta OMA' can} \right)
\end{array} \right.\\
\Rightarrow 2\alpha = \widehat {OA'M} + \widehat {OMA'} = 2\widehat {OA'M}\\
\Rightarrow \widehat {OA'M} = \alpha \\
\Rightarrow AM = AA'\sin \widehat {AA'M} = 2\sin \alpha \\
\Rightarrow A{M^2} = 4{\sin ^2}\alpha
\end{array}\)
Vậy:
\(\begin{array}{l}
\Rightarrow 2\left({1 - \cos 2\alpha } \right) = 4{\sin ^2}\alpha \\
\Leftrightarrow 1 - \cos 2\alpha = 2{\sin ^2}\alpha \\
\Leftrightarrow \cos 2\alpha = 1 - 2{\sin ^2}\alpha
\end{array}\)
Cách khác:
Áp dụng định lý cosin trong tam giác OAM. Ta có:
$A M^{2}=O M^{2}+O A^{2}-2 O M . O A \cdot \cos 2 \alpha=2-2 \cos 2 \alpha(1)$
Trong tam giác vuông AMA', ta có:
$A M^{2}=A A^{\prime 2}-A^{\prime} M^{2}=4 O A^{2}-A^{\prime} M^{2}=4-A^{\prime} M^{2}$ (2)
Trong tam giác MA'O ta có: $O M^{2}=A^{\prime} M^{2}+O A^{\prime 2}-2 A^{\prime} M . O A^{\prime} \cos \alpha$
$=>A^{\prime} M^{2}=2 A^{\prime} M \cos \alpha=>A^{\prime} M=2 \cos \alpha$ (3)
Thay (3) vào (2) ta có: $A M^{2}=4-4 \cos ^{2} \alpha$ (4)
Từ (1) và (4) ta có:
$2-2 \cos 2 \alpha=4-4 \cos ^{2} \alpha=>\cos 2 \alpha=1-2 \sin ^{2} \alpha$ (5)
sin2α = 2sinα cosα
Lời giải chi tiết:
Ta có: \({S_{A'MA}} = {1 \over 2}AA'. MH = MH = \sin 2\alpha \)
Lại có:
\({S_{A'MA}} = {1 \over 2}A'M. AM \) \(= {1 \over 2}A'A\cos \alpha. A'A\sin \alpha \)
\(= 2\sin \alpha \cos \alpha \)
Vậy: \(\sin2α = 2\sinα \cosα\)
Phương pháp giải:
Sử dụng công thức nhân đôi vừa chứng minh ở câu a, b.
Xuất phát từ \(\cos \frac{\pi }{4},\sin \frac{\pi }{4}\) để tính \(\cos \frac{\pi }{8},\sin \frac{\pi }{8}\).
Lời giải chi tiết:
Ta có: \(\cos {\pi \over 4} = 1 - 2{\sin ^2}{\pi \over 8}\) nên:
\(\eqalign{
& {\sin ^2}{\pi \over 8} = {1 \over 2}(1 - {{\sqrt 2 } \over 2}) = {{2 - \sqrt 2 } \over 4} \cr
& \sin {\pi \over 8} = {{\sqrt {2 - \sqrt 2 } } \over 2} \cr
&\cos \frac{\pi }{8} = \sqrt {1 - {{\sin }^2}\frac{\pi }{8}} \cr &= \sqrt {1 - \frac{{2 - \sqrt 2 }}{4}} = \frac{{\sqrt {2 + \sqrt 2 } }}{2} \cr
& {{3\pi } \over 8} = {\pi \over 2} - {\pi \over 8} \cr &\Rightarrow \left\{ \matrix{
\cos {{3\pi } \over 8} = \sin {\pi \over 8} = {{\sqrt {2 - \sqrt 2 } } \over 2} \hfill \cr
\sin {{3\pi } \over 8} = \cos {\pi \over 8} = {{\sqrt {2 + \sqrt 2 } } \over 2} \hfill \cr
\tan {{3\pi } \over 8} = \cot {\pi \over 8} = \sqrt 2 + 1 \hfill \cr
\cot {{3\pi } \over 8} = \tan {\pi \over 8} = \sqrt 2 - 1 \hfill \cr} \right. \cr
& {{5\pi } \over 8} = {\pi \over 2} + {\pi \over 8} \cr &\Rightarrow \left\{ \matrix{
\cos {{5\pi } \over 8} = - \sin {\pi \over 8} = {{\sqrt {2 - \sqrt 2 } } \over 2} \hfill \cr
\sin {{5\pi } \over 8} = \cos {\pi \over 8} = {{\sqrt {2 + \sqrt 2 } } \over 2} \hfill \cr
\tan {{5\pi } \over 8} = - \cot {\pi \over 8} = - \sqrt 2 - 1 \hfill \cr
\cot {{5\pi } \over 8} = - \tan {\pi \over 8} = 1 - \sqrt 2 \hfill \cr} \right. \cr} \)
Câu a
Tính AM2 bằng hai cách khác nhau để suy ra: cos2α = 1 – 2sin2αLời giải chi tiết:

Ta có:
\(\eqalign{
& A{M^2} = \overline {AH} .\overline {{\rm{AA}}} {\rm{' = (}}\overline {AO} + \overline {OH}).\overline {{\rm{AA}}'} \cr
& = (- 1 + \cos 2\alpha)(- 2) = 2(1 - \cos 2\alpha) \cr} \)
Lại có:
\(\begin{array}{l}
\left\{ \begin{array}{l}
2\alpha = \widehat {AOM} = \widehat {OA'M} + \widehat {OMA'}\\
\widehat {OA'M} = \widehat {OMA'}\left({\Delta OMA' can} \right)
\end{array} \right.\\
\Rightarrow 2\alpha = \widehat {OA'M} + \widehat {OMA'} = 2\widehat {OA'M}\\
\Rightarrow \widehat {OA'M} = \alpha \\
\Rightarrow AM = AA'\sin \widehat {AA'M} = 2\sin \alpha \\
\Rightarrow A{M^2} = 4{\sin ^2}\alpha
\end{array}\)
Vậy:
\(\begin{array}{l}
\Rightarrow 2\left({1 - \cos 2\alpha } \right) = 4{\sin ^2}\alpha \\
\Leftrightarrow 1 - \cos 2\alpha = 2{\sin ^2}\alpha \\
\Leftrightarrow \cos 2\alpha = 1 - 2{\sin ^2}\alpha
\end{array}\)
Cách khác:
Áp dụng định lý cosin trong tam giác OAM. Ta có:
$A M^{2}=O M^{2}+O A^{2}-2 O M . O A \cdot \cos 2 \alpha=2-2 \cos 2 \alpha(1)$
Trong tam giác vuông AMA', ta có:
$A M^{2}=A A^{\prime 2}-A^{\prime} M^{2}=4 O A^{2}-A^{\prime} M^{2}=4-A^{\prime} M^{2}$ (2)
Trong tam giác MA'O ta có: $O M^{2}=A^{\prime} M^{2}+O A^{\prime 2}-2 A^{\prime} M . O A^{\prime} \cos \alpha$
$=>A^{\prime} M^{2}=2 A^{\prime} M \cos \alpha=>A^{\prime} M=2 \cos \alpha$ (3)
Thay (3) vào (2) ta có: $A M^{2}=4-4 \cos ^{2} \alpha$ (4)
Từ (1) và (4) ta có:
$2-2 \cos 2 \alpha=4-4 \cos ^{2} \alpha=>\cos 2 \alpha=1-2 \sin ^{2} \alpha$ (5)
Câu b
Tính diện tích tam giác A’MA bằng hai cách khác nhau để suy ra:sin2α = 2sinα cosα
Lời giải chi tiết:
Ta có: \({S_{A'MA}} = {1 \over 2}AA'. MH = MH = \sin 2\alpha \)
Lại có:
\({S_{A'MA}} = {1 \over 2}A'M. AM \) \(= {1 \over 2}A'A\cos \alpha. A'A\sin \alpha \)
\(= 2\sin \alpha \cos \alpha \)
Vậy: \(\sin2α = 2\sinα \cosα\)
Câu c
Chứng minh: \(\sin {\pi \over 8} = {1 \over 2}\sqrt {2 - \sqrt 2 } ;\) \(\cos {\pi \over 8} = {1 \over 2}\sqrt {2 + \sqrt 2 } \) rồi tính các giá trị lượng giác của các góc \({{3\pi } \over 8}\) và \({{5\pi } \over 8}\)Phương pháp giải:
Sử dụng công thức nhân đôi vừa chứng minh ở câu a, b.
Xuất phát từ \(\cos \frac{\pi }{4},\sin \frac{\pi }{4}\) để tính \(\cos \frac{\pi }{8},\sin \frac{\pi }{8}\).
Lời giải chi tiết:
Ta có: \(\cos {\pi \over 4} = 1 - 2{\sin ^2}{\pi \over 8}\) nên:
\(\eqalign{
& {\sin ^2}{\pi \over 8} = {1 \over 2}(1 - {{\sqrt 2 } \over 2}) = {{2 - \sqrt 2 } \over 4} \cr
& \sin {\pi \over 8} = {{\sqrt {2 - \sqrt 2 } } \over 2} \cr
&\cos \frac{\pi }{8} = \sqrt {1 - {{\sin }^2}\frac{\pi }{8}} \cr &= \sqrt {1 - \frac{{2 - \sqrt 2 }}{4}} = \frac{{\sqrt {2 + \sqrt 2 } }}{2} \cr
& {{3\pi } \over 8} = {\pi \over 2} - {\pi \over 8} \cr &\Rightarrow \left\{ \matrix{
\cos {{3\pi } \over 8} = \sin {\pi \over 8} = {{\sqrt {2 - \sqrt 2 } } \over 2} \hfill \cr
\sin {{3\pi } \over 8} = \cos {\pi \over 8} = {{\sqrt {2 + \sqrt 2 } } \over 2} \hfill \cr
\tan {{3\pi } \over 8} = \cot {\pi \over 8} = \sqrt 2 + 1 \hfill \cr
\cot {{3\pi } \over 8} = \tan {\pi \over 8} = \sqrt 2 - 1 \hfill \cr} \right. \cr
& {{5\pi } \over 8} = {\pi \over 2} + {\pi \over 8} \cr &\Rightarrow \left\{ \matrix{
\cos {{5\pi } \over 8} = - \sin {\pi \over 8} = {{\sqrt {2 - \sqrt 2 } } \over 2} \hfill \cr
\sin {{5\pi } \over 8} = \cos {\pi \over 8} = {{\sqrt {2 + \sqrt 2 } } \over 2} \hfill \cr
\tan {{5\pi } \over 8} = - \cot {\pi \over 8} = - \sqrt 2 - 1 \hfill \cr
\cot {{5\pi } \over 8} = - \tan {\pi \over 8} = 1 - \sqrt 2 \hfill \cr} \right. \cr} \)
Rất tiếc, câu hỏi này chưa có lời giải chi tiết. Bạn ơi, đăng nhập và giải chi tiết giúp zix.vn nhé!!!