Câu hỏi: Trong hệ tọa độ vuông góc Oxy gắn với một đường tròn lượng giác, cho điểm P có tọa độ (2, -3)
Lời giải chi tiết:
Ta có:
\(\left\{ \matrix{
\overrightarrow {OM} \uparrow \uparrow \overrightarrow {OP} \hfill \cr
|\overrightarrow {OM} | = |{{\overrightarrow {OP} } \over {\overrightarrow {OP} }}| = {{|\overrightarrow {OP} |} \over {|\overrightarrow {OP} |}}=1 \hfill \cr} \right. \)
Vậy M là giao của tia OP với đường tròn lượng giác.
Cách khác:
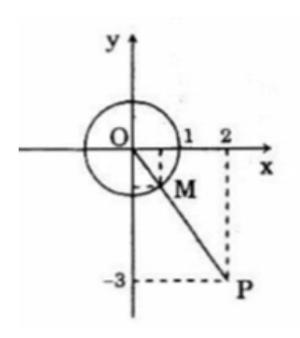
a) Gọi $\mathrm{M}\left(x_{0} ; y_{0}\right)$ thì ta có $\overrightarrow{O M}\left(x_{0} ; y_{0}\right)$ từ giả thiết đã cho ta có:
$$
\left\{\begin{array}{c}
x_{0}=\frac{1}{O P} \cdot 2=\frac{2}{\sqrt{13}} \\
y_{0}=\frac{1}{O P} \cdot(-3)=-\frac{3}{\sqrt{13}}
\end{array}\right.
$$
Vậy $\mathrm{M}\left(\frac{2}{\sqrt{13}} ;-\frac{3}{\sqrt{13}}\right)$
Đường tròn lượng giác đối với Oxy có phương trình :
$x^{2}+y^{2}=1,$ dễ thấy tọa độ $\mathrm{M}$ thoả mãn phương trình đường tròn nên ta có (đpcm)
Lời giải chi tiết:
Ta có:
\(\eqalign{
& |\overrightarrow {OP} | = \sqrt {{2^2} + {{(- 3)}^2}} = \sqrt {13} \cr
& \Rightarrow \overrightarrow {OM} ({2 \over {\sqrt {13} }}; - {3 \over {\sqrt {13} }}) \cr} \)
Vậy
\(\left\{ \matrix{
\cos (Ox, OP) = {2 \over {\sqrt {13} }} \hfill \cr
sin(Ox, OP) = {{ - 3} \over {\sqrt {13} }} \hfill \cr} \right.\)
Câu a
Chứng minh rằng điểm M sao cho \(\overrightarrow {OM} = {{\overrightarrow {OP} } \over {|\overrightarrow {OP} |}}\) là giao điểm của tia OP với đường tròn lượng giác đóLời giải chi tiết:
Ta có:
\(\left\{ \matrix{
\overrightarrow {OM} \uparrow \uparrow \overrightarrow {OP} \hfill \cr
|\overrightarrow {OM} | = |{{\overrightarrow {OP} } \over {\overrightarrow {OP} }}| = {{|\overrightarrow {OP} |} \over {|\overrightarrow {OP} |}}=1 \hfill \cr} \right. \)
Vậy M là giao của tia OP với đường tròn lượng giác.
Cách khác:

a) Gọi $\mathrm{M}\left(x_{0} ; y_{0}\right)$ thì ta có $\overrightarrow{O M}\left(x_{0} ; y_{0}\right)$ từ giả thiết đã cho ta có:
$$
\left\{\begin{array}{c}
x_{0}=\frac{1}{O P} \cdot 2=\frac{2}{\sqrt{13}} \\
y_{0}=\frac{1}{O P} \cdot(-3)=-\frac{3}{\sqrt{13}}
\end{array}\right.
$$
Vậy $\mathrm{M}\left(\frac{2}{\sqrt{13}} ;-\frac{3}{\sqrt{13}}\right)$
Đường tròn lượng giác đối với Oxy có phương trình :
$x^{2}+y^{2}=1,$ dễ thấy tọa độ $\mathrm{M}$ thoả mãn phương trình đường tròn nên ta có (đpcm)
Câu b
Tính tọa độ điểm M và từ đó suy ra cosin, sin của góc lượng giác (Ox, OP)Lời giải chi tiết:
Ta có:
\(\eqalign{
& |\overrightarrow {OP} | = \sqrt {{2^2} + {{(- 3)}^2}} = \sqrt {13} \cr
& \Rightarrow \overrightarrow {OM} ({2 \over {\sqrt {13} }}; - {3 \over {\sqrt {13} }}) \cr} \)
Vậy
\(\left\{ \matrix{
\cos (Ox, OP) = {2 \over {\sqrt {13} }} \hfill \cr
sin(Ox, OP) = {{ - 3} \over {\sqrt {13} }} \hfill \cr} \right.\)
Rất tiếc, câu hỏi này chưa có lời giải chi tiết. Bạn ơi, đăng nhập và giải chi tiết giúp zix.vn nhé!!!