Câu hỏi: Cho hình chóp S. ABCD có đáy là hình thoi. \(\widehat A = {120^0}, B{\rm{D}} = a\), cạnh bên SA vuông góc với đáy, góc giữa mặt phẳng (SBC) và mặt phẳng đáy là 60°. Tính:
a) Đường cao của hình chóp.
b) Khoảng cách từ A đến mặt phẳng (SCB).
a) Đường cao của hình chóp.
b) Khoảng cách từ A đến mặt phẳng (SCB).
Lời giải chi tiết
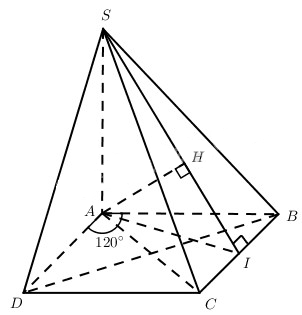
A) Vì ABCD là hình thoi và \(\widehat {BA{\rm{D}}} = {120^0}\) nên ABC là tam giác đều. Gọi I là trung điểm của BC thì \(BC \bot \left( {AIS} \right)\).
Mặt khác SAI là tam giác vuông tại A nên \(\widehat {SIA}\) là góc giữa hai mặt phẳng (SBC) và mặt phẳng đáy (ABCD). Theo giả thiết \(\widehat {SIA} = {60^0}\).
Ta có \(B{{\rm{D}}^2} + A{C^2} = 4{\rm{A}}{B^2}\).
mà AC = AB nên
\(AB = {{B{\rm{D}}} \over {\sqrt 3 }} = {a \over {\sqrt 3 }} \Rightarrow AI = {a \over {\sqrt 3 }}.{{\sqrt 3 } \over 2} = {a \over 2}\).
Vì \(SA \bot \left( {ABC{\rm{D}}} \right)\) nên SA là đường cao của hình chóp S. ABCD. Ta có :
\(SA = AI.\tan {60^0}\).
Vậy \(SA = {a \over 2}\sqrt 3 \).
b) Ta có \(BC \bot \left( {SAI} \right)\), từ đó \(\left( {SAI} \right) \bot \left({SBC} \right)\). Vậy nếu kẻ đường cao AH của tam giác SAI thì AH là khoảng cách từ A đến mp(SBC). Xét tam giác vuông SAI ta có:
\(AH = {{SA. AI} \over {SI}} = {{{{a\sqrt 3 } \over 2}.{a \over 2}} \over {\sqrt {{{3{{\rm{a}}^2}} \over 4} + {{{a^2}} \over 4}} }} = {{a\sqrt 3 } \over 4}.\)
Vậy khoảng cách từ A đến mặt phẳng (SCB) bằng \({{a\sqrt 3 } \over 4}\).
A) Vì ABCD là hình thoi và \(\widehat {BA{\rm{D}}} = {120^0}\) nên ABC là tam giác đều. Gọi I là trung điểm của BC thì \(BC \bot \left( {AIS} \right)\).
Mặt khác SAI là tam giác vuông tại A nên \(\widehat {SIA}\) là góc giữa hai mặt phẳng (SBC) và mặt phẳng đáy (ABCD). Theo giả thiết \(\widehat {SIA} = {60^0}\).
Ta có \(B{{\rm{D}}^2} + A{C^2} = 4{\rm{A}}{B^2}\).
mà AC = AB nên
\(AB = {{B{\rm{D}}} \over {\sqrt 3 }} = {a \over {\sqrt 3 }} \Rightarrow AI = {a \over {\sqrt 3 }}.{{\sqrt 3 } \over 2} = {a \over 2}\).
Vì \(SA \bot \left( {ABC{\rm{D}}} \right)\) nên SA là đường cao của hình chóp S. ABCD. Ta có :
\(SA = AI.\tan {60^0}\).
Vậy \(SA = {a \over 2}\sqrt 3 \).
b) Ta có \(BC \bot \left( {SAI} \right)\), từ đó \(\left( {SAI} \right) \bot \left({SBC} \right)\). Vậy nếu kẻ đường cao AH của tam giác SAI thì AH là khoảng cách từ A đến mp(SBC). Xét tam giác vuông SAI ta có:
\(AH = {{SA. AI} \over {SI}} = {{{{a\sqrt 3 } \over 2}.{a \over 2}} \over {\sqrt {{{3{{\rm{a}}^2}} \over 4} + {{{a^2}} \over 4}} }} = {{a\sqrt 3 } \over 4}.\)
Vậy khoảng cách từ A đến mặt phẳng (SCB) bằng \({{a\sqrt 3 } \over 4}\).