Câu hỏi: Trong mặt phẳng (P) cho đường tròn (C) đường kính AB = 2R; C là điểm bất kì thuộc đường tròn (C không trùng với A, B). S là điểm trong không gian sao cho SA vuông góc với (P) và SA = h (h cho trước và h < 2R). Gọi I và J lần lượt là trung điểm của AC và SB. Hãy xác định vị trí điểm C trên đường tròn để IJ là đường vuông góc chung của AC và SB. Khi đó, tính khoảng cách từ điểm A đến mp(SBC).
Lời giải chi tiết
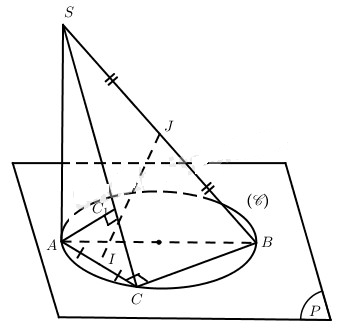
Cách 1:
Dễ thấy ACB là tam giác vuông tại C mà \(SA \bot \left( {ABC} \right)\) nên \(\widehat {SCB} = {90^0}\). Tam giác SAB vuông tại A, tam giác SCB vuông tại C mà J là trung điểm của SB, từ đó AJ = CJ. Mặt khác IA = IC. Vậy \(IJ \bot AC\). Từ đó, IJ là đường vuông góc chung của AC và SB khi và chỉ khi IS = IB. Xét các tam giác vuông SAI và BCI ta thấy IS = IB khi và chỉ khi SA = BC.
Vậy điểm C thuộc đường tròn đã cho sao cho BC = h thì IJ là đường vuông góc chung của AC và SB. Chú ý rằng có hai điểm C như vậy.
Cách 2:
Xét tứ diện SABC với I, J là trung điểm của AC, SB ta có IJ là đường vuông góc chung của AC và SB khi và chỉ khi SA = CB và SC = AB.
Xét các tam giác vuông SAC và ACB ta có các đẳng thức trên xảy ra khi và chỉ khi SA = BC.
Dễ thấy \(d\left( {A; mp\left( {SCB} \right)} \right) = A{C_1}\), trong đó AC1 là đường cao của tam giác vuông SAC.
Ta có \(A{C_1} = {{SA. AC} \over {SC}}\)
mà \(AC = \sqrt {4{{\rm{R}}^2} - {h^2}} , SC = 2{\rm{R}}\)
Từ đó, ta có \(A{C_1} = {{h\sqrt {4{{\rm{R}}^2} - {h^2}} } \over {2{\rm{R}}}}\)
Cách 1:
Dễ thấy ACB là tam giác vuông tại C mà \(SA \bot \left( {ABC} \right)\) nên \(\widehat {SCB} = {90^0}\). Tam giác SAB vuông tại A, tam giác SCB vuông tại C mà J là trung điểm của SB, từ đó AJ = CJ. Mặt khác IA = IC. Vậy \(IJ \bot AC\). Từ đó, IJ là đường vuông góc chung của AC và SB khi và chỉ khi IS = IB. Xét các tam giác vuông SAI và BCI ta thấy IS = IB khi và chỉ khi SA = BC.
Vậy điểm C thuộc đường tròn đã cho sao cho BC = h thì IJ là đường vuông góc chung của AC và SB. Chú ý rằng có hai điểm C như vậy.
Cách 2:
Xét tứ diện SABC với I, J là trung điểm của AC, SB ta có IJ là đường vuông góc chung của AC và SB khi và chỉ khi SA = CB và SC = AB.
Xét các tam giác vuông SAC và ACB ta có các đẳng thức trên xảy ra khi và chỉ khi SA = BC.
Dễ thấy \(d\left( {A; mp\left( {SCB} \right)} \right) = A{C_1}\), trong đó AC1 là đường cao của tam giác vuông SAC.
Ta có \(A{C_1} = {{SA. AC} \over {SC}}\)
mà \(AC = \sqrt {4{{\rm{R}}^2} - {h^2}} , SC = 2{\rm{R}}\)
Từ đó, ta có \(A{C_1} = {{h\sqrt {4{{\rm{R}}^2} - {h^2}} } \over {2{\rm{R}}}}\)