Câu hỏi: Tính thể tích khối tứ diện ABCD có các cặp cạnh đối bằng nhau :
\(AB=CD=a, AC=BD=b, AD=BC=c\)
\(AB=CD=a, AC=BD=b, AD=BC=c\)
Lời giải chi tiết
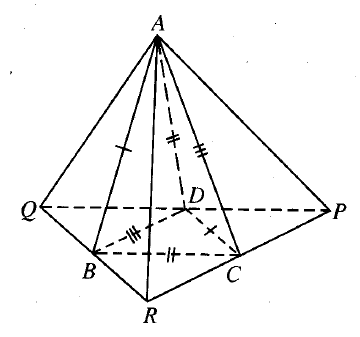
Dựng tứ diện APQR sao cho B, C, D lần lượt là trung điểm của các cạnh QR, RP, PQ.
Ta có \(AD = BC = {1 \over 2}PQ\) mà D là trung điểm của PQ nên \(AQ \bot {\rm{AP}}{\rm{.}}\)
Chứng minh tương tự, ta cũng có \(AQ \bot {\rm{AR}},{\rm{AR}} \bot AP.\)
Dễ thấy :
\({V_{ABCD}} = {1 \over 4}{V_{APQR}} = {1 \over 4}.{1 \over 6}. AP. AQ.{\rm{AR}}( *)\)
Xét các tam giác vuông \(APQ, AQR, ARP,\) ta có
\(A{P^2} + A{Q^2} = 4{c^2},\)
\(A{Q^2} + {\rm{A}}{{\rm{R}}^2} = 4{a^2},\)
\({\rm{A}}{{\rm{R}}^2} + A{P^2} = 4{b^2}.\)
Từ đó suy ra :
\(\eqalign{ & AP = \sqrt 2 .\sqrt { - {a^2} + {b^2} + {c^2}} ,\cr&AQ = \sqrt 2 \sqrt {{a^2} - {b^2} + {c^2}} , \cr & {\rm{A}}{{\rm{R}}} = \sqrt 2 \sqrt {{a^2} + {b^2} - {c^2}} . \cr} \)
Vậy từ \(\left( * \right)\) ta suy ra :
${V_{ABCD}} = \frac{{\sqrt 2 }}{{12}}\sqrt {\left( { - {a^2} + {b^2} + {c^2}} \right).\left( {{a^2} - {b^2} + {c^2}} \right)\left( {{a^2} + {b^2} - {c^2}} \right)} $
Dựng tứ diện APQR sao cho B, C, D lần lượt là trung điểm của các cạnh QR, RP, PQ.
Ta có \(AD = BC = {1 \over 2}PQ\) mà D là trung điểm của PQ nên \(AQ \bot {\rm{AP}}{\rm{.}}\)
Chứng minh tương tự, ta cũng có \(AQ \bot {\rm{AR}},{\rm{AR}} \bot AP.\)
Dễ thấy :
\({V_{ABCD}} = {1 \over 4}{V_{APQR}} = {1 \over 4}.{1 \over 6}. AP. AQ.{\rm{AR}}( *)\)
Xét các tam giác vuông \(APQ, AQR, ARP,\) ta có
\(A{P^2} + A{Q^2} = 4{c^2},\)
\(A{Q^2} + {\rm{A}}{{\rm{R}}^2} = 4{a^2},\)
\({\rm{A}}{{\rm{R}}^2} + A{P^2} = 4{b^2}.\)
Từ đó suy ra :
\(\eqalign{ & AP = \sqrt 2 .\sqrt { - {a^2} + {b^2} + {c^2}} ,\cr&AQ = \sqrt 2 \sqrt {{a^2} - {b^2} + {c^2}} , \cr & {\rm{A}}{{\rm{R}}} = \sqrt 2 \sqrt {{a^2} + {b^2} - {c^2}} . \cr} \)
Vậy từ \(\left( * \right)\) ta suy ra :
${V_{ABCD}} = \frac{{\sqrt 2 }}{{12}}\sqrt {\left( { - {a^2} + {b^2} + {c^2}} \right).\left( {{a^2} - {b^2} + {c^2}} \right)\left( {{a^2} + {b^2} - {c^2}} \right)} $