Câu hỏi: Cho đoạn thẳng \(AB,\) điểm \(C\) nằm giữa \(A\) và \(B.\) Vẽ về một phía của \(AB\) các nửa đường tròn có đường kính theo thứ tự là \(AB, AC, CB.\) Đường vuông góc với \(AB\) tại \(C\) cắt nửa đường tròn lớn tại \(D.\) \(DA, DB\) cắt các nửa đường tròn có đường kính \(AC, CB\) theo thứ tự \(M, N.\)
\(a)\) Tứ giác \(DMCN\) là hình gì\(?\) Vì sao \(?\)
\(b)\) Chứng minh hệ thức \(DM.DA = DN.DB.\)
\(c)\) Chứng minh rằng \(MN\) là tiếp tuyến chung của các nửa đường tròn có đường kính \(AC\) và \(CB.\)
\(d)\) Điểm \(C\) ở vị trí nào trên \(AB\) thì \(MN\) có độ dài lớn nhất \(?\)
\(a)\) Tứ giác \(DMCN\) là hình gì\(?\) Vì sao \(?\)
\(b)\) Chứng minh hệ thức \(DM.DA = DN.DB.\)
\(c)\) Chứng minh rằng \(MN\) là tiếp tuyến chung của các nửa đường tròn có đường kính \(AC\) và \(CB.\)
\(d)\) Điểm \(C\) ở vị trí nào trên \(AB\) thì \(MN\) có độ dài lớn nhất \(?\)
Phương pháp giải
Sử dụng kiến thức:
+) Tứ giác có ba góc vuông là hình chữ nhật.
+) Hệ thức lượng trong tam giác vuông: Bình phương cạnh góc vuông bằng tích cạnh huyền với hình chiếu cạnh góc vuông đó trên cạnh huyền.
+) Trong hình chữ nhật, hai đường chéo cắt nhau tại trung điểm mỗi đường.
+) Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.
Lời giải chi tiết
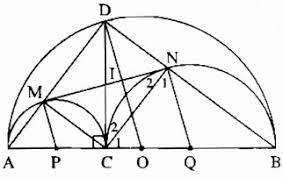
\(a)\) Tam giác \(ABD\) nội tiếp trong đường tròn có \(AB\) là đường kính nên \(\widehat {BDA} = 90^\circ \) hay \(\widehat {MDN} = 90^\circ \)
Tam giác \(ACM\) nội tiếp đường tròn có \(AC\) là đường kính nên \(\widehat {AMC} = 90^\circ \)
Suy ra: \(CM ⊥ AD ⇒\widehat {CMD} = 90^\circ \)
Tam giác \(BCN\) nội tiếp trong đường tròn có \(BC\) là đường kính nên \(\widehat {BNC} = 90^\circ \)
Suy ra: \(CN ⊥ BD ⇒ \widehat {CND} = 90^\circ \)
Tứ giác \(CMDN\) có ba góc vuông nên nó là hình chữ nhật.
\(b)\) Tam giác \(ACD\) vuông tại \(C\) có \(CM ⊥ AD.\)
Theo hệ thức lượng trong tam giác vuông, ta có:
\(C{D^2} = DM.DA\) \((1)\)
Tam giác \(BCD\) vuông tại \(C\) có \(CN ⊥ BD.\)
Theo hệ thức lượng trong tam giác vuông, ta có:
\(C{D^2} = DN.DB\) \((2)\)
Từ \((1)\) và \((2)\) suy ra: \(DM.DA = DN.DB\)
\(c)\) Gọi \(P\) là trung điểm của \(AC, Q\) là trung điểm của \(BC, I\) là giao điểm của \(MN\) với \(DC.\)
Vì \(CMDN\) là hình chữ nhật nên \(IC = IM = ID = IN\)
Tam giác \(CNI\) cân tại \(I\) nên \(\widehat {ICN} = \widehat {INC}\) \((3)\)
Tam giác \(CNQ\) cân tại \(Q\) nên \(\widehat {QCN} = \widehat {QNC}\) \((4)\)
Vì \(AB ⊥ CD\) nên \(\widehat {ICN} + \widehat {QCN} = 90^\circ \) \((5)\)
Từ \((3), (4)\) và \((5)\) suy ra: \(\widehat {INC} + \widehat {QNC} = 90^\circ \) hay \(MN ⊥ QN\)
Vậy \(MN\) là tiếp tuyến của đường tròn đường kính \(BC.\)
Tam giác \(CMI\) cân tại \(I\) nên \(\widehat {ICM} = \widehat {IMC}\) \((6)\)
Tam giác \(CMP\) cân tại \(P\) nên \(\widehat {PCM} = \widehat {PMC}\) \((7)\)
Vì \(AB ⊥ CD\) nên \(\widehat {PCM} + \widehat {ICM} = 90^\circ \) \( (8)\)
Từ \((6), (7)\) và \((8)\) suy ra: \(\widehat {PMC} + \widehat {IMC} = 90^\circ \) hay \(MN ⊥ PM\)
Vậy \(MN\) là tiếp tuyến của đường tròn đường kính \(AC.\)
\(d)\) Gọi \(O\) là trung điểm của \(AB\)
Tứ giác \(CMDN\) là hình chữ nhật nên \(CD = MN\)
Trong tam giác \(OCD\) ta có: \(CD \le OD\) nên \(MN \le OD\)
Vì \(OD\) không đổi nên \(MN = OD\) là giá trị lớn nhất khi và chỉ khi \(C\) trùng với \(O.\)
Vậy \(C\) là trung điểm của \(AB\) thì \(MN\) có độ dài lớn nhất.
Sử dụng kiến thức:
+) Tứ giác có ba góc vuông là hình chữ nhật.
+) Hệ thức lượng trong tam giác vuông: Bình phương cạnh góc vuông bằng tích cạnh huyền với hình chiếu cạnh góc vuông đó trên cạnh huyền.
+) Trong hình chữ nhật, hai đường chéo cắt nhau tại trung điểm mỗi đường.
+) Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.
Lời giải chi tiết
\(a)\) Tam giác \(ABD\) nội tiếp trong đường tròn có \(AB\) là đường kính nên \(\widehat {BDA} = 90^\circ \) hay \(\widehat {MDN} = 90^\circ \)
Tam giác \(ACM\) nội tiếp đường tròn có \(AC\) là đường kính nên \(\widehat {AMC} = 90^\circ \)
Suy ra: \(CM ⊥ AD ⇒\widehat {CMD} = 90^\circ \)
Tam giác \(BCN\) nội tiếp trong đường tròn có \(BC\) là đường kính nên \(\widehat {BNC} = 90^\circ \)
Suy ra: \(CN ⊥ BD ⇒ \widehat {CND} = 90^\circ \)
Tứ giác \(CMDN\) có ba góc vuông nên nó là hình chữ nhật.
\(b)\) Tam giác \(ACD\) vuông tại \(C\) có \(CM ⊥ AD.\)
Theo hệ thức lượng trong tam giác vuông, ta có:
\(C{D^2} = DM.DA\) \((1)\)
Tam giác \(BCD\) vuông tại \(C\) có \(CN ⊥ BD.\)
Theo hệ thức lượng trong tam giác vuông, ta có:
\(C{D^2} = DN.DB\) \((2)\)
Từ \((1)\) và \((2)\) suy ra: \(DM.DA = DN.DB\)
\(c)\) Gọi \(P\) là trung điểm của \(AC, Q\) là trung điểm của \(BC, I\) là giao điểm của \(MN\) với \(DC.\)
Vì \(CMDN\) là hình chữ nhật nên \(IC = IM = ID = IN\)
Tam giác \(CNI\) cân tại \(I\) nên \(\widehat {ICN} = \widehat {INC}\) \((3)\)
Tam giác \(CNQ\) cân tại \(Q\) nên \(\widehat {QCN} = \widehat {QNC}\) \((4)\)
Vì \(AB ⊥ CD\) nên \(\widehat {ICN} + \widehat {QCN} = 90^\circ \) \((5)\)
Từ \((3), (4)\) và \((5)\) suy ra: \(\widehat {INC} + \widehat {QNC} = 90^\circ \) hay \(MN ⊥ QN\)
Vậy \(MN\) là tiếp tuyến của đường tròn đường kính \(BC.\)
Tam giác \(CMI\) cân tại \(I\) nên \(\widehat {ICM} = \widehat {IMC}\) \((6)\)
Tam giác \(CMP\) cân tại \(P\) nên \(\widehat {PCM} = \widehat {PMC}\) \((7)\)
Vì \(AB ⊥ CD\) nên \(\widehat {PCM} + \widehat {ICM} = 90^\circ \) \( (8)\)
Từ \((6), (7)\) và \((8)\) suy ra: \(\widehat {PMC} + \widehat {IMC} = 90^\circ \) hay \(MN ⊥ PM\)
Vậy \(MN\) là tiếp tuyến của đường tròn đường kính \(AC.\)
\(d)\) Gọi \(O\) là trung điểm của \(AB\)
Tứ giác \(CMDN\) là hình chữ nhật nên \(CD = MN\)
Trong tam giác \(OCD\) ta có: \(CD \le OD\) nên \(MN \le OD\)
Vì \(OD\) không đổi nên \(MN = OD\) là giá trị lớn nhất khi và chỉ khi \(C\) trùng với \(O.\)
Vậy \(C\) là trung điểm của \(AB\) thì \(MN\) có độ dài lớn nhất.