Google
Câu hỏi: Cho tam giác $ABC$ có $A\left( 2; 2; 3 \right), B\left( 1;3; 3 \right), C\left( 1; 2; 4 \right)$. Các tia $Bu, Cv$ vuông góc với mặt phẳng $\left( ABC \right)$ và nằm cùng phía đối với mặt phẳng ấy. Các điểm $M,N$ di động tương ứng trên các tia $Bu, Cv$ sao cho $BM+CN=MN$. Gọi trực tâm $H$ tam giác $AMN$, biết $H$ nằm trên một đường tròn $\left( C \right)$ cố định. Tính bán kính của đường tròn $\left( C \right)$.
A. $\dfrac{3\sqrt{2}}{8}$.
B. $\dfrac{3\sqrt{2}}{4}$.
C. $\dfrac{5\sqrt{2}}{8}$.
D. $\dfrac{2\sqrt{2}}{3}$.
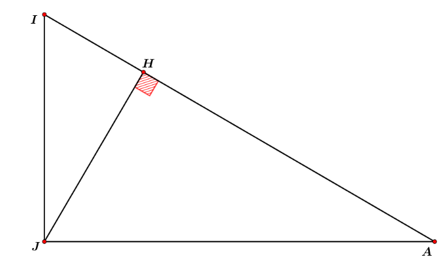
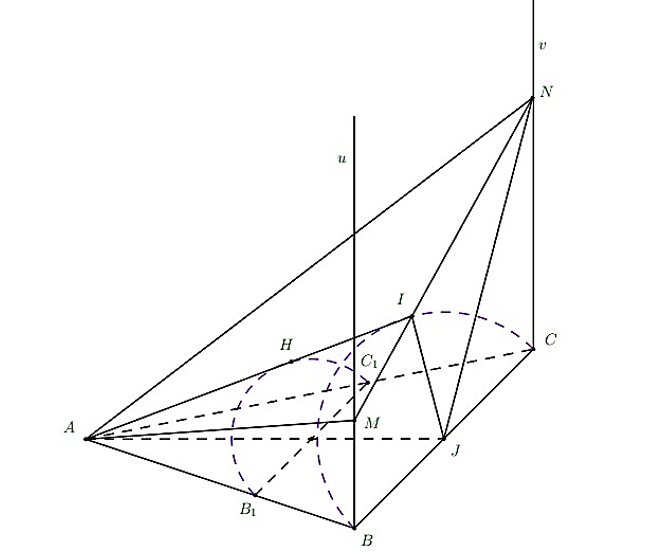Lấy $I$ trên tia $MN$ sao cho $MI=BM\Rightarrow IN=CN$. Các tam giác $MBI, NCI$ cân suy ra
$\widehat{NIC}+\widehat{MIB}=\dfrac{{{180}^{{}^\circ }}-\widehat{INC}}{2}+\dfrac{{{180}^{{}^\circ }}-\widehat{IMB}}{2}=\dfrac{{{360}^{{}^\circ }}-(\widehat{INC}+\widehat{IMB})}{2}={{90}^{{}^\circ }}$. Vậy ta có
$\widehat{BIC}={{180}^{{}^\circ }}-(\widehat{NIC}+\widehat{MIB})={{90}^{{}^\circ }}$. Hay $I$ thuộc nửa đường tròn đường kính $BC$. Ta cũng có
$\widehat{MJN}={{90}^{{}^\circ }}$ và $AJ\bot \left( BC,Bx \right)\Rightarrow AJ\bot JM,AJ\bot JN$. Vậy $J.AMN$ tam diện vuông nên
$JH\bot \left( AMN \right)$.
Chứng minh 3 điểm $A$, $H$, $I$ thẳng hàng:
Vì các tam giác $\Delta IMB$, $\Delta JIB$ cân tại $M$ và $I$ nên $\widehat{MIB}=\widehat{MBI}$ và $\widehat{JIB}=\widehat{JBI}$
$\Rightarrow \widehat{MIB}+\widehat{JIB}=\widehat{MBI}+\widehat{JBI}=\widehat{MBJ}={{90}^{\circ }}$ (Vì $Bu\bot \left( ABC \right)$.
$\Rightarrow \widehat{MIJ}={{90}^{\circ }}\Rightarrow JI\bot MN$
Mà $JH\bot \left( AMN \right)$, do đó theo định lí ba đường vuông góc suy ra $HI\bot MN$.
Ta có $\left\{ \begin{aligned}
& HI\bot MN \\
& AH\bot MN \\
\end{aligned} \right. $ suy ra ba điểm $ A $, $ H $, $ I$ thẳng hàng.
Ta có $HI$ là hình chiếu vuông góc của $JI$ lên mặt phẳng $\left( AMN \right)$, mà
Ta nhận thấy tam giác $ABC$ đều cạnh $a=\sqrt{2}\Rightarrow AJ=\dfrac{\sqrt{3}}{2}a$.
Ta có $\Delta ABJ=\Delta AIJ\Rightarrow AB=AI=a$ và $AH=\dfrac{A{{J}^{2}}}{AI}=\dfrac{3a}{4}\Rightarrow \dfrac{AH}{AI}=\dfrac{3}{4}\Rightarrow \overrightarrow{AH}=\dfrac{3}{4}\overrightarrow{AI}$. Vậy $H$ là ảnh của $I$ qua phép vị tự tâm $A$, tỉ số $\dfrac{3}{4}$. Ta có bán kính của đường tròn $\left( C \right)$ là
$R=\dfrac{3}{4}BJ=\dfrac{3}{4}.\dfrac{\sqrt{2}}{2}=\dfrac{3\sqrt{2}}{8}$.
A. $\dfrac{3\sqrt{2}}{8}$.
B. $\dfrac{3\sqrt{2}}{4}$.
C. $\dfrac{5\sqrt{2}}{8}$.
D. $\dfrac{2\sqrt{2}}{3}$.
$\widehat{NIC}+\widehat{MIB}=\dfrac{{{180}^{{}^\circ }}-\widehat{INC}}{2}+\dfrac{{{180}^{{}^\circ }}-\widehat{IMB}}{2}=\dfrac{{{360}^{{}^\circ }}-(\widehat{INC}+\widehat{IMB})}{2}={{90}^{{}^\circ }}$. Vậy ta có
$\widehat{BIC}={{180}^{{}^\circ }}-(\widehat{NIC}+\widehat{MIB})={{90}^{{}^\circ }}$. Hay $I$ thuộc nửa đường tròn đường kính $BC$. Ta cũng có
$\widehat{MJN}={{90}^{{}^\circ }}$ và $AJ\bot \left( BC,Bx \right)\Rightarrow AJ\bot JM,AJ\bot JN$. Vậy $J.AMN$ tam diện vuông nên
$JH\bot \left( AMN \right)$.
Chứng minh 3 điểm $A$, $H$, $I$ thẳng hàng:
Vì các tam giác $\Delta IMB$, $\Delta JIB$ cân tại $M$ và $I$ nên $\widehat{MIB}=\widehat{MBI}$ và $\widehat{JIB}=\widehat{JBI}$
$\Rightarrow \widehat{MIB}+\widehat{JIB}=\widehat{MBI}+\widehat{JBI}=\widehat{MBJ}={{90}^{\circ }}$ (Vì $Bu\bot \left( ABC \right)$.
$\Rightarrow \widehat{MIJ}={{90}^{\circ }}\Rightarrow JI\bot MN$
Mà $JH\bot \left( AMN \right)$, do đó theo định lí ba đường vuông góc suy ra $HI\bot MN$.
Ta có $\left\{ \begin{aligned}
& HI\bot MN \\
& AH\bot MN \\
\end{aligned} \right. $ suy ra ba điểm $ A $, $ H $, $ I$ thẳng hàng.
Ta có $HI$ là hình chiếu vuông góc của $JI$ lên mặt phẳng $\left( AMN \right)$, mà
Ta nhận thấy tam giác $ABC$ đều cạnh $a=\sqrt{2}\Rightarrow AJ=\dfrac{\sqrt{3}}{2}a$.
Ta có $\Delta ABJ=\Delta AIJ\Rightarrow AB=AI=a$ và $AH=\dfrac{A{{J}^{2}}}{AI}=\dfrac{3a}{4}\Rightarrow \dfrac{AH}{AI}=\dfrac{3}{4}\Rightarrow \overrightarrow{AH}=\dfrac{3}{4}\overrightarrow{AI}$. Vậy $H$ là ảnh của $I$ qua phép vị tự tâm $A$, tỉ số $\dfrac{3}{4}$. Ta có bán kính của đường tròn $\left( C \right)$ là
$R=\dfrac{3}{4}BJ=\dfrac{3}{4}.\dfrac{\sqrt{2}}{2}=\dfrac{3\sqrt{2}}{8}$.
Đáp án A.
