Câu hỏi: Cho hai đường tròn (O; R) và (O’; R’) nằm trên hai mặt phẳng song song (P) và (Q) sao cho OO’ vuông góc với (P). Đặt OO’ = h. Chứng minh rằng có mặt cầu đi qua hai đường tròn trên, tính diện tích mặt cầu đó.
Lời giải chi tiết
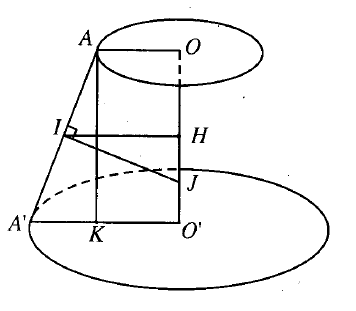
Giả sử \(R \le R'\). Vì \(OO' \bot (P)\) nên mọi điểm thuộc OO’ cách đều các điểm của đường tròn (O; R), đồng thời cách đều các điểm của đường tròn (O’; R’),
Xét mp(R) qua OO’ và hai mặt phẳng (P), (Q) theo hai giao tuyến OA, O’A', \(A \in (O; R), A' \in (O'; R').\)
Trong mp(R) , đường trung trực AA’ cắt OO’ tại J. Khi đó, mặt cầu tâm J, bán kính JA đi qua cả hai đường tròn (O; R) và (O’; R’).
Gọi S là diện tích mặt cầu đó thì
\(S = 4\pi. J{A^2} = 4\pi (O{A^2} + J{O^2}) \)\(= 4\pi ({R^2} + J{O^2}).\)
Kẻ IH song song với \(AO(H \in OO')\) thì \(OH = {h \over 2}\).
Từ OH+JH=JO, suy ra \({h \over 2} + JH = JO.\)
Kẻ AK song song với OO’(\((K \in O'A')\) thì có \({{HJ} \over {A'K}} = {{IH} \over {AK}},\) từ đó
\(HJ = {{{{R' + R} \over 2}.(R' - R)} \over h} = {{R{'^2} - {R^2}} \over {2h}}.\)
Vậy \(JO = {h \over 2} + {{R{'^2} - {R^2}} \over {2h}} = {{{h^2} + R{'^2} - {R^2}} \over {2h}}\) và diện tích mặt cầu phải tìm là
\(\eqalign{ & S = 4\pi \left[ {{R^2} + {{{{\left( {{h^2} + R{'^2} - {R^2}} \right)}^2}} \over {4{h^2}}}} \right] \cr & = \pi .{{4{R^2}{h^2} + ({h^2} + R{'^2} - {R^2})^2} \over {{h^2}}}. \cr} \)
Giả sử \(R \le R'\). Vì \(OO' \bot (P)\) nên mọi điểm thuộc OO’ cách đều các điểm của đường tròn (O; R), đồng thời cách đều các điểm của đường tròn (O’; R’),
Xét mp(R) qua OO’ và hai mặt phẳng (P), (Q) theo hai giao tuyến OA, O’A', \(A \in (O; R), A' \in (O'; R').\)
Trong mp(R) , đường trung trực AA’ cắt OO’ tại J. Khi đó, mặt cầu tâm J, bán kính JA đi qua cả hai đường tròn (O; R) và (O’; R’).
Gọi S là diện tích mặt cầu đó thì
\(S = 4\pi. J{A^2} = 4\pi (O{A^2} + J{O^2}) \)\(= 4\pi ({R^2} + J{O^2}).\)
Kẻ IH song song với \(AO(H \in OO')\) thì \(OH = {h \over 2}\).
Từ OH+JH=JO, suy ra \({h \over 2} + JH = JO.\)
Kẻ AK song song với OO’(\((K \in O'A')\) thì có \({{HJ} \over {A'K}} = {{IH} \over {AK}},\) từ đó
\(HJ = {{{{R' + R} \over 2}.(R' - R)} \over h} = {{R{'^2} - {R^2}} \over {2h}}.\)
Vậy \(JO = {h \over 2} + {{R{'^2} - {R^2}} \over {2h}} = {{{h^2} + R{'^2} - {R^2}} \over {2h}}\) và diện tích mặt cầu phải tìm là
\(\eqalign{ & S = 4\pi \left[ {{R^2} + {{{{\left( {{h^2} + R{'^2} - {R^2}} \right)}^2}} \over {4{h^2}}}} \right] \cr & = \pi .{{4{R^2}{h^2} + ({h^2} + R{'^2} - {R^2})^2} \over {{h^2}}}. \cr} \)