Google
Câu hỏi: Xét hai số phức $z, \mathrm{w}$ thỏa mẵn $|z-3-i|=1$ và $|\mathrm{w}-1|=|\mathrm{w}+i|$. Giá trị nhỏ nhất của $P=$ $|w+1-3 i|+|w-z|$ bằng
A. $P_{\min }=\sqrt{13}$.
B. $P_{\min }=2 \sqrt{5}-1$.
C. $P_{\min }=5$.
D. $P_{\min }=7$.
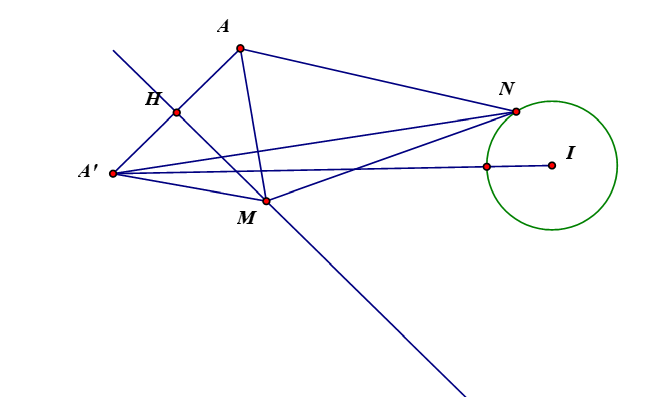$|z-3-i|=1 \Rightarrow$ tập hợp điểm $N$ biểu diễn số phức $z$ là đường tròn tâm $I(3 ; 1)$ bán kính $R=1$
$|\mathrm{w}-1|=|\mathrm{w}+i| \Rightarrow$ tập hợp điểm $M$ biểu diễn số phức $\mathrm{w}$ là đường thẳng $d: x+y=0$
Gọi $A=(-1 ; 3), A^{\prime}$ là điểm đối xứng với $A$ qua $d$
Ta có $P=|\mathrm{w}+1-3 i|+|\mathrm{w}-z|=M A+M N=M A^{\prime}+M N \geq A^{\prime} N \geq A^{\prime} I-R$
Gọi $d^{\prime}$ là đường thẳng đi qua $A$ và vuông góc với $d$
Phương trình đường thẳng $d^{\prime}$ có dạng $x-y+m=0$
Vì $A \in d^{\prime}$ nên $m=4$.
Phương trình đường thẳng $d^{\prime}$ là $x-y+4=0$
Gọi $H$ là giao điểm của $d$ và $d^{\prime}$.
$A^{\prime}$ đối xứng với $A$ qua $d$ nên $H$ là trung điểm của $A A^{\prime}$ suy ra tọa độ của $A^{\prime}=(-3 ; 1)$ $A^{\prime} I=6$
Vậy $P_{\min }^{\text {min }}=5$. Dấu bằng xảy ra khi và chỉ khi $A^{\prime}, M, N, I$ thẳng hàng.
A. $P_{\min }=\sqrt{13}$.
B. $P_{\min }=2 \sqrt{5}-1$.
C. $P_{\min }=5$.
D. $P_{\min }=7$.
$|\mathrm{w}-1|=|\mathrm{w}+i| \Rightarrow$ tập hợp điểm $M$ biểu diễn số phức $\mathrm{w}$ là đường thẳng $d: x+y=0$
Gọi $A=(-1 ; 3), A^{\prime}$ là điểm đối xứng với $A$ qua $d$
Ta có $P=|\mathrm{w}+1-3 i|+|\mathrm{w}-z|=M A+M N=M A^{\prime}+M N \geq A^{\prime} N \geq A^{\prime} I-R$
Gọi $d^{\prime}$ là đường thẳng đi qua $A$ và vuông góc với $d$
Phương trình đường thẳng $d^{\prime}$ có dạng $x-y+m=0$
Vì $A \in d^{\prime}$ nên $m=4$.
Phương trình đường thẳng $d^{\prime}$ là $x-y+4=0$
Gọi $H$ là giao điểm của $d$ và $d^{\prime}$.
$A^{\prime}$ đối xứng với $A$ qua $d$ nên $H$ là trung điểm của $A A^{\prime}$ suy ra tọa độ của $A^{\prime}=(-3 ; 1)$ $A^{\prime} I=6$
Vậy $P_{\min }^{\text {min }}=5$. Dấu bằng xảy ra khi và chỉ khi $A^{\prime}, M, N, I$ thẳng hàng.
Đáp án C.