Xét các số phức $z$ và $w$ thay đổi thỏa mãn $|z-2+2 i|=2$ và...

Với $z=x+y i(x, y \in \mathbb{R})$, ta có
$
|z-2+2 i|=2 \Leftrightarrow|x-2+(y+2) i|=2 \Leftrightarrow(x-2)^2+(y+2)^2=4 \text {. }
$
Do đó, trong mặt phẳng $O x y$ gọi $M(x, y)$ là điểm biểu diễn số phức $z$. Khi đó, $M$ thuộc đường tròn (C) tâm $I(2 ;-2)$, bán kính $R=2$.
Với $w=a+b i(a, b \in \mathbb{R})$, ta có
$
\begin{aligned}
& |w-i|=|w+2-3 i| \Leftrightarrow|a+(b-1) i|=|a+2+(b-3) i| \\
& \Leftrightarrow \sqrt{a^2+(b-1)^2}=\sqrt{(a+2)^2+(b-3)^2} \Leftrightarrow a-b+3=0 .
\end{aligned}
$
Do đó, trong mặt phẳng $O x y$ gọi $N(a ; b)$ là điểm biểu diễn số phức $w$. Khi đó $N$ thuộc đường thẳng $d: x-y+3=0$.
Ta có $P=|z-w|+|w-3+i|=N M+A N$ với $A(3 ;-1)$.
Vì $\left(x_A-y_A+3\right)\left(x_I-y_I+3\right)>0$ nên hai điểm $A$ và $I$ nằm cùng phía với đường thẳng $d$.
Mặt khác $d(I, d)=\dfrac{7 \sqrt{2}}{2}>2$ nên đường thẳng $d$ và đường tròn $(C)$ không có điểm chung.
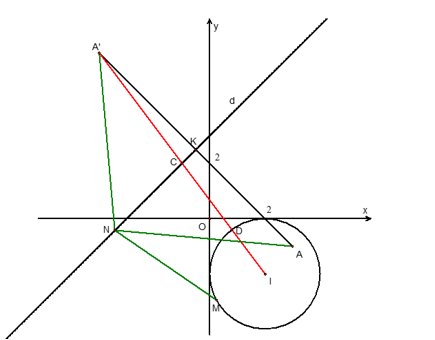Gọi $A^{\prime}$ là điểm đối xứng với $A$ qua đường thẳng $d$. Ta có đường thẳng $A A^{\prime}$ đi qua điểm $A(3 ;-1)$ và vuông góc với đường thẳng $d$ nên có phương trình: $x+y-2=0$.
Gọi $K=A A^{\prime} \cap d \Rightarrow K\left(-\dfrac{1}{2} ; \dfrac{5}{2}\right)$.
Vì $A^{\prime}$ đối xứng với $A$ qua đường thẳng $d$ nên $K$ là trung điểm của $A A^{\prime}$, suy $\operatorname{ra} A^{\prime}(-4 ; 6)$.
Gọi $C, D$ lần lượt là giao điểm của đoạn thẳng $I A^{\prime}$ với đường thẳng $d$ và đường tròn $(C)$.
Ta có $P=N A+N M=N A^{\prime}+N M \geq A^{\prime} M \geq A^{\prime} D=I A^{\prime}-R=8$.
$\Rightarrow \min P=8$
Dấu bằng xảy ra khi và chỉ khi $N \equiv C$ và $M \equiv D$.
Vậy $\min P=8$.