Câu hỏi: Cho hai số phức $z ; w$ thoả mãn $z \cdot \bar{z}=1$ và $|w-3+4 i|=2$. Tìm giá trị lớn nhất của biểu thức $P=$ $|z-w|$.
A. $P_{\max }=10$.
B. $P_{\max }=5+\sqrt{2}$.
C. $P_{\max }=5$.
D. $P_{\max }=8$.
A. $P_{\max }=10$.
B. $P_{\max }=5+\sqrt{2}$.
C. $P_{\max }=5$.
D. $P_{\max }=8$.
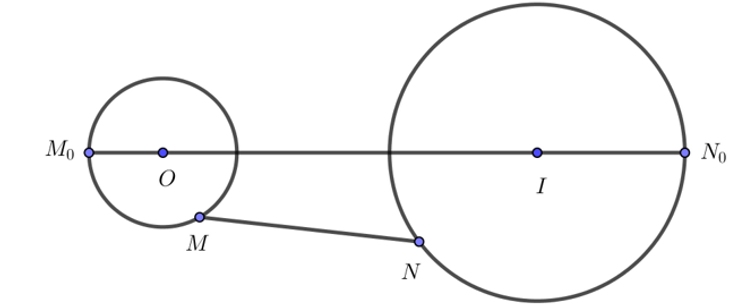
Gọi $M(x ; y)$ là điểm biểu diễn của số phức $z$.
$z \cdot \bar{z}=1 \Leftrightarrow x^2+y^2=1 \Rightarrow M \in\left(C_1\right)$ có tâm $O(0 ; 0)$, bán kính $R_1=1$.
Gọi $N$ là điểm biểu diễn của số phức $\mathrm{w}$.
$|\mathrm{w}-3+4 i|=2 \Rightarrow N \in\left(C_2\right):(x-3)^2+(y+4)^2=4$, có tâm $I(3 ;-4)$, bán kính $R_2=2$.
Do $O I=5>R_1+R_2 \Rightarrow\left(C_1\right) ;\left(C_2\right)$ nằm ngoài nhau.
 $
$
P=|z-\mathrm{w}|=M N \text {. Do đó } P_{\max } \Leftrightarrow M N_{\max } \Leftrightarrow M N=M_0 N_0=O I+R_1+R_2=8 \text {. Vậy } P_{\max }=8
$
$z \cdot \bar{z}=1 \Leftrightarrow x^2+y^2=1 \Rightarrow M \in\left(C_1\right)$ có tâm $O(0 ; 0)$, bán kính $R_1=1$.
Gọi $N$ là điểm biểu diễn của số phức $\mathrm{w}$.
$|\mathrm{w}-3+4 i|=2 \Rightarrow N \in\left(C_2\right):(x-3)^2+(y+4)^2=4$, có tâm $I(3 ;-4)$, bán kính $R_2=2$.
Do $O I=5>R_1+R_2 \Rightarrow\left(C_1\right) ;\left(C_2\right)$ nằm ngoài nhau.
P=|z-\mathrm{w}|=M N \text {. Do đó } P_{\max } \Leftrightarrow M N_{\max } \Leftrightarrow M N=M_0 N_0=O I+R_1+R_2=8 \text {. Vậy } P_{\max }=8
$
Đáp án D.