Google
Câu hỏi: Cho các số phức $z$ và $w$ thỏa mãn $(3-i)|z|=\dfrac{z}{w-1}+1-i$. Tìm giá trị lớn nhất $T=|w+i|$.
A. $\dfrac{1}{2}$.
B. $\dfrac{\sqrt{2}}{2}$.
C. $\dfrac{3 \sqrt{2}}{2}$.
D. 2 .
A. $\dfrac{1}{2}$.
B. $\dfrac{\sqrt{2}}{2}$.
C. $\dfrac{3 \sqrt{2}}{2}$.
D. 2 .
Đk: $w \neq 1$.
Ta có:
$(3-i)|z|=\dfrac{z}{w-1}+1-i \Leftrightarrow(3-i)|z|-1+i=\dfrac{z}{w-1} \Leftrightarrow w=\dfrac{z}{(3|z|-1)+(1-|z|) i}+1$.
Vậy $T=|w+i|=\left|\dfrac{z}{(3|z|-1)+(1-|z|) i}+1+i\right| \leq\left|\dfrac{z}{(3|z|-1)+(1-|z|) i}\right|+|1+i| \leq \dfrac{|z|}{\sqrt{10|z|^2-8|z|+2}}+\sqrt{2}$.
Đặt $t=|z|$ điều kiện: $t \geq 0$. Xét hàm số $f(t)=\dfrac{t}{\sqrt{10 t^2-8 t+2}}+\sqrt{2}$.
$f^{\prime}(t)=\dfrac{-4 t+2}{\left(10 t^2-8 t+2\right) \sqrt{10 t^2-8 t+2}} ; f^{\prime}(t)=0 \Leftrightarrow t=\dfrac{1}{2}$.
BBT
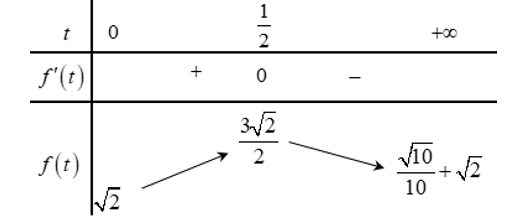Dựa vào bảng biến thiên ta có $T=|w+i| \leq \max _{[0 ;+\infty)} f(t)=f\left(\dfrac{1}{2}\right)=\dfrac{3 \sqrt{2}}{2}$.
Ta có:
$(3-i)|z|=\dfrac{z}{w-1}+1-i \Leftrightarrow(3-i)|z|-1+i=\dfrac{z}{w-1} \Leftrightarrow w=\dfrac{z}{(3|z|-1)+(1-|z|) i}+1$.
Vậy $T=|w+i|=\left|\dfrac{z}{(3|z|-1)+(1-|z|) i}+1+i\right| \leq\left|\dfrac{z}{(3|z|-1)+(1-|z|) i}\right|+|1+i| \leq \dfrac{|z|}{\sqrt{10|z|^2-8|z|+2}}+\sqrt{2}$.
Đặt $t=|z|$ điều kiện: $t \geq 0$. Xét hàm số $f(t)=\dfrac{t}{\sqrt{10 t^2-8 t+2}}+\sqrt{2}$.
$f^{\prime}(t)=\dfrac{-4 t+2}{\left(10 t^2-8 t+2\right) \sqrt{10 t^2-8 t+2}} ; f^{\prime}(t)=0 \Leftrightarrow t=\dfrac{1}{2}$.
BBT
Đáp án C.
