Google
Câu hỏi: Cho các số phức $w, z$ thỏa mãn $|w+i|=\dfrac{3 \sqrt{5}}{5}$ và $5 w=(2+i)(z-4)$. Giá trị lớn nhất của biểu thức $P=|z-1-2 i|+|z-5-2 i|$ bằng
A. $4 \sqrt{13}$.
B. $6 \sqrt{7}$.
C. $4+2 \sqrt{13}$.
D. $2 \sqrt{53}$.
A. $4 \sqrt{13}$.
B. $6 \sqrt{7}$.
C. $4+2 \sqrt{13}$.
D. $2 \sqrt{53}$.
Gọi $z=x+y i$, với $x, y \in \mathbb{R}$. Khi đó $M(x ; y)$ là điểm biểu diễn cho số phức $z$.
Theo giả thiết, $5 w=(2+i)(z-4) \Leftrightarrow 5(w+i)=(2+i)(z-4)+5 i \Leftrightarrow(2-i)(w+i)=z-$ $3+2 i$
$\Leftrightarrow|z-3+2 i|=3$. Suy ra $M(x ; y)$ thuộc đường tròn $(C):(x-3)^2+(y+2)^2=9$.
Ta có $P=|z-1-2 i|+|z-5-2 i|=M A+M B$, với $A(1 ; 2)$ và $B(5 ; 2)$.
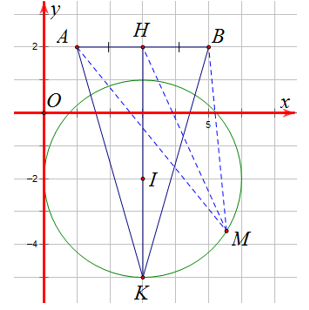Gọi $H$ là trung điểm của $A B$, ta có $H(3 ; 2)$ và khi đó:
$
P=M A+M B \leq \sqrt{2\left(M A^2+M B^2\right)} \text { hay } P \leq \sqrt{4 M H^2+A B^2} \text {. }
$
Mặt khác, $M H \leq K H$ với mọi $M \in(C)$ nên
$
P \leq \sqrt{4 K H^2+A B^2}=\sqrt{4(I H+R)^2+A B^2}=2 \sqrt{53} \text {. }
$
Vậy $P_{\text {max }}=2 \sqrt{53}$ khi $\left\{\begin{array}{l}M \equiv K \\ M A=M B\end{array}\right.$ hay $z=3-5 i$ và $\mathrm{w}=\dfrac{3}{5}-\dfrac{11}{5} \mathrm{i}$.
Theo giả thiết, $5 w=(2+i)(z-4) \Leftrightarrow 5(w+i)=(2+i)(z-4)+5 i \Leftrightarrow(2-i)(w+i)=z-$ $3+2 i$
$\Leftrightarrow|z-3+2 i|=3$. Suy ra $M(x ; y)$ thuộc đường tròn $(C):(x-3)^2+(y+2)^2=9$.
Ta có $P=|z-1-2 i|+|z-5-2 i|=M A+M B$, với $A(1 ; 2)$ và $B(5 ; 2)$.
$
P=M A+M B \leq \sqrt{2\left(M A^2+M B^2\right)} \text { hay } P \leq \sqrt{4 M H^2+A B^2} \text {. }
$
Mặt khác, $M H \leq K H$ với mọi $M \in(C)$ nên
$
P \leq \sqrt{4 K H^2+A B^2}=\sqrt{4(I H+R)^2+A B^2}=2 \sqrt{53} \text {. }
$
Vậy $P_{\text {max }}=2 \sqrt{53}$ khi $\left\{\begin{array}{l}M \equiv K \\ M A=M B\end{array}\right.$ hay $z=3-5 i$ và $\mathrm{w}=\dfrac{3}{5}-\dfrac{11}{5} \mathrm{i}$.
Đáp án D.