Google
Câu hỏi: Cho các số phức $z,w$ thỏa mãn $\left| w-3+i \right|=3\sqrt{2}$ và $\dfrac{w}{z-2}=1+i$. Giá trị lớn nhất của biểu thức $P=\left| z-1-2i \right|+\left| z-5-2i \right|$ bằng
A. $\sqrt{52}+\sqrt{55}$.
B. $3+\sqrt{134}$.
C. $\dfrac{29}{2}$.
D. $2\sqrt{53}$.
A. $\sqrt{52}+\sqrt{55}$.
B. $3+\sqrt{134}$.
C. $\dfrac{29}{2}$.
D. $2\sqrt{53}$.
Ta có: $\dfrac{w}{z-2}=1+i\Rightarrow w=\left( z-2 \right)\left( 1+i \right)\Leftrightarrow w-3+i=\left( 1+i \right)z-5-i\Rightarrow \left| \left( 1+i \right)z-5-i \right|=3\sqrt{2}.$
$\Rightarrow \left| 1+i \right|\left| z+\dfrac{-5-i}{1+i} \right|=3\sqrt{2}\Leftrightarrow \left| z-3+2i \right|=3$. Nên $M\left( z \right)$ thuộc đường tròn tâm $I\left( 3;-2 \right),R=3.$
Ta có: $P=\left| z-1-2i \right|+\left| z-5-2i \right|=MA+MB$, với $M\left( z \right),A\left( 1;2 \right),B\left( 5;2 \right)$.
Khi đó: ${{P}^{2}}={{\left( MA+MB \right)}^{2}}\le 2\left( M{{A}^{2}}+M{{B}^{2}} \right)=2.\left( 2M{{C}^{2}}+\dfrac{A{{B}^{2}}}{2} \right)=A{{B}^{2}}+4M{{C}^{2}}=16+4M{{C}^{2}}$
Với $C\left( 3;2 \right)$ là trung điểm của đoạn thẳng $AB.$
$\Rightarrow P$ đạt giá trị lớn nhất khi $MC$ lớn nhất.
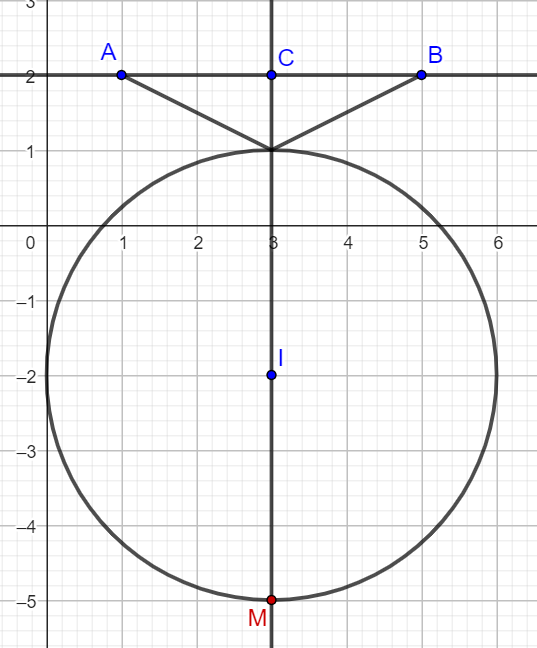Dễ thấy $MC$ lớn nhất khi điểm $M$ ở vị trí như hình vẽ, nên:
${{P}^{2}}\le 16+4.49=212\Rightarrow P\le 2\sqrt{53}$.
$\Rightarrow \left| 1+i \right|\left| z+\dfrac{-5-i}{1+i} \right|=3\sqrt{2}\Leftrightarrow \left| z-3+2i \right|=3$. Nên $M\left( z \right)$ thuộc đường tròn tâm $I\left( 3;-2 \right),R=3.$
Ta có: $P=\left| z-1-2i \right|+\left| z-5-2i \right|=MA+MB$, với $M\left( z \right),A\left( 1;2 \right),B\left( 5;2 \right)$.
Khi đó: ${{P}^{2}}={{\left( MA+MB \right)}^{2}}\le 2\left( M{{A}^{2}}+M{{B}^{2}} \right)=2.\left( 2M{{C}^{2}}+\dfrac{A{{B}^{2}}}{2} \right)=A{{B}^{2}}+4M{{C}^{2}}=16+4M{{C}^{2}}$
Với $C\left( 3;2 \right)$ là trung điểm của đoạn thẳng $AB.$
$\Rightarrow P$ đạt giá trị lớn nhất khi $MC$ lớn nhất.
${{P}^{2}}\le 16+4.49=212\Rightarrow P\le 2\sqrt{53}$.
Đáp án D.