Google
Câu hỏi: Cho hai số phức $z, w$ thỏa mãn $\left| w+i \right|=\dfrac{3}{\sqrt{10}}$ và $10w=\left( 3-i \right)\left( z-3 \right)$. Giá trị lớn nhất của biểu thức $P=\left| z-2-i \right|+\left| z-6-i \right|$ bằng
A. $3+\sqrt{10}$.
B. $2\sqrt{58}$.
C. $3\sqrt{10}$.
D. $2\sqrt{53}$
A. $3+\sqrt{10}$.
B. $2\sqrt{58}$.
C. $3\sqrt{10}$.
D. $2\sqrt{53}$
Ta có: $10w=\left( 3-i \right)\left( z-3 \right)\Leftrightarrow 10\left( w+i \right)=\left( 3-i \right)\left( z-3 \right)+10i$
Môđun hai vế ta được: $\begin{aligned}
& \left| 10\left( w+i \right) \right|=\left| \left( 3-i \right)\left( z-3 \right)+10i \right|\Leftrightarrow 10\left| \left( w+i \right) \right|=\left| \left( 3-i \right)\left[ \left( z-3 \right)+\dfrac{10i}{3-i} \right] \right| \\
& \Leftrightarrow 10.\dfrac{3}{\sqrt{10}}=\left| \left( 3-i \right)\left[ \left( z-3 \right)-1+3i \right] \right|\Leftrightarrow 3\sqrt{10}=\left| 3-i \right|.\left| z-4+3i \right|\Leftrightarrow 3\sqrt{10}=\sqrt{10}.\left| z-4+3i \right| \\
& \Leftrightarrow \left| z-4+3i \right|=3 \\
\end{aligned}$
Đặt $z=x+yi \left( x,y\in \mathbb{R} \right)$ có điểm biểu diễn là $M\left( x;y \right)$.
Khi đó $\left| z-4+3i \right|=3\Leftrightarrow {{\left( x-4 \right)}^{2}}+{{\left( y+3 \right)}^{2}}=9$ nên tập hợp điểm biểu diễn số phức $z$ là một đường tròn $\left( C \right)$ có tâm $I=\left( 4;-3 \right)$ và bán kính bằng $R=3$.
Ta có: $P=\left| z-2-i \right|+\left| z-6-i \right|=\left| z-\left( 2+i \right) \right|+\left| z-\left( 6+i \right) \right|=MA+MB$ với $A\left( 2;1 \right); B\left( 6;1 \right)$.
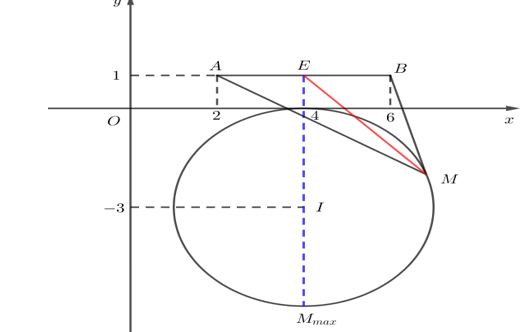Gọi $E$ là trung điểm của đoạn thẳng $AB$, suy ra $E=\left( 4;1 \right)$.
Xét tam giác $MAB$ ta có: $M{{E}^{2}}=\dfrac{2\left( M{{A}^{2}}+M{{B}^{2}} \right)-A{{B}^{2}}}{4}\Rightarrow 2\left( M{{A}^{2}}+M{{B}^{2}} \right)=4M{{E}^{2}}+A{{B}^{2}}=4M{{E}^{2}}+16$.
Ta có:
${{P}^{2}}={{\left( MA+MB \right)}^{2}}={{\left( 1.MA+1.MB \right)}^{2}}\le \left( {{1}^{2}}+{{1}^{2}} \right)\left( M{{A}^{2}}+M{{B}^{2}} \right)=2\left( M{{A}^{2}}+M{{B}^{2}} \right)=4M{{E}^{2}}+16$.
Suy ra ${{P}^{2}}\le 4M{{E}^{2}}+16\le 4{{\left( I{{M}_{\max }}+IE \right)}^{2}}+16=4{{\left( 3+4 \right)}^{2}}+16=212\Rightarrow P\le \sqrt{212}=2\sqrt{53}$.
Vậy GTLN của biểu thức $P$ là $2\sqrt{53}$.
Môđun hai vế ta được: $\begin{aligned}
& \left| 10\left( w+i \right) \right|=\left| \left( 3-i \right)\left( z-3 \right)+10i \right|\Leftrightarrow 10\left| \left( w+i \right) \right|=\left| \left( 3-i \right)\left[ \left( z-3 \right)+\dfrac{10i}{3-i} \right] \right| \\
& \Leftrightarrow 10.\dfrac{3}{\sqrt{10}}=\left| \left( 3-i \right)\left[ \left( z-3 \right)-1+3i \right] \right|\Leftrightarrow 3\sqrt{10}=\left| 3-i \right|.\left| z-4+3i \right|\Leftrightarrow 3\sqrt{10}=\sqrt{10}.\left| z-4+3i \right| \\
& \Leftrightarrow \left| z-4+3i \right|=3 \\
\end{aligned}$
Đặt $z=x+yi \left( x,y\in \mathbb{R} \right)$ có điểm biểu diễn là $M\left( x;y \right)$.
Khi đó $\left| z-4+3i \right|=3\Leftrightarrow {{\left( x-4 \right)}^{2}}+{{\left( y+3 \right)}^{2}}=9$ nên tập hợp điểm biểu diễn số phức $z$ là một đường tròn $\left( C \right)$ có tâm $I=\left( 4;-3 \right)$ và bán kính bằng $R=3$.
Ta có: $P=\left| z-2-i \right|+\left| z-6-i \right|=\left| z-\left( 2+i \right) \right|+\left| z-\left( 6+i \right) \right|=MA+MB$ với $A\left( 2;1 \right); B\left( 6;1 \right)$.
Xét tam giác $MAB$ ta có: $M{{E}^{2}}=\dfrac{2\left( M{{A}^{2}}+M{{B}^{2}} \right)-A{{B}^{2}}}{4}\Rightarrow 2\left( M{{A}^{2}}+M{{B}^{2}} \right)=4M{{E}^{2}}+A{{B}^{2}}=4M{{E}^{2}}+16$.
Ta có:
${{P}^{2}}={{\left( MA+MB \right)}^{2}}={{\left( 1.MA+1.MB \right)}^{2}}\le \left( {{1}^{2}}+{{1}^{2}} \right)\left( M{{A}^{2}}+M{{B}^{2}} \right)=2\left( M{{A}^{2}}+M{{B}^{2}} \right)=4M{{E}^{2}}+16$.
Suy ra ${{P}^{2}}\le 4M{{E}^{2}}+16\le 4{{\left( I{{M}_{\max }}+IE \right)}^{2}}+16=4{{\left( 3+4 \right)}^{2}}+16=212\Rightarrow P\le \sqrt{212}=2\sqrt{53}$.
Vậy GTLN của biểu thức $P$ là $2\sqrt{53}$.
Đáp án D.
