Trong không gian với hệ trục tọa độ $O x y z$, gọi $(P)$ là mặt...

Cách 1:
Đường thẳng $d$ qua điểm $M(1 ;-2 ; 0)$, có véc tơ chỉ phương $\vec{a}=(1 ;-1 ;-2)$ và trục $O y$ có véc tơ chỉ phương $\vec{J}=(0 ; 1 ; 0)$.
Gọi $\vec{n}=(A ; B ; C)\left(A^2+B^2+C^2 \neq 0\right)$ là một véc tơ pháp tuyến của mặt phẳng $(P)$.
Vì $d \subset(P) \Rightarrow \vec{a} \cdot \vec{n}=0 \Leftrightarrow 1 \cdot A+(-1) \cdot B+(-2) \cdot C=0 \Leftrightarrow A=B+2 C \Rightarrow \vec{n}=(B+2 C ; B ; C)$.
Gọi $\varphi$ là góc giữa mặt phẳng $(P)$ và trục $O y\left(0 \leq \varphi \leq \dfrac{\pi}{2}\right)$.
Ta có $\sin \varphi=\dfrac{|\vec{n} \cdot \vec{j}|}{|\vec{n}| \cdot|\vec{j}|}=\dfrac{|B|}{\sqrt{(B+2 C)^2+B^2+C^2}}=\sqrt{\dfrac{B^2}{2 B^2+4 B C+5 C^2}}$
$
=\sqrt{\dfrac{1}{2+4 \cdot\left(\dfrac{C}{B}\right)+5\left(\dfrac{C}{B}\right)^2}}=\sqrt{\dfrac{1}{5\left(\dfrac{C}{B}+\dfrac{2}{5}\right)^2+\dfrac{6}{5}}}(B \neq 0) \text {. }
$
Vì hàm số $\sin \varphi$ tăng liên tục trên $\left(0 ; \dfrac{\pi}{2}\right)$ nên $\varphi$ đạt giá trị lớn nhất khi $\sin \varphi$ lớn nhất Lúc đó $5\left(\dfrac{C}{B}+\dfrac{2}{5}\right)^2+\dfrac{6}{5}$ đạt giá trị nhỏ nhất bằng $\dfrac{6}{5}$ khi và chỉ khi $\dfrac{C}{B}+\dfrac{2}{5}=0$.
Chọn $B=5 \Rightarrow C=-2 ; A=1 \Rightarrow \vec{n}=(1 ; 5 ;-2)$.
Phương trình mặt phẳng $(P)$ qua điểm $M(1 ;-2 ; 0)$, có véc tơ pháp tuyến $\vec{n}=(1 ; 5 ;-2)$ là 1 . $(x-$ 1) $+5 \cdot(y+2)-2(z-0)=0 \Leftrightarrow x+5 y-2 z+9=0$.
Thế tọa độ $N(-1 ;-2 ;-1)$ vào phương trình mặt phẳng $(P):-1+5(-2)-2(-1)+9=0$ (luôn đúng).
Vậy điểm $N(-1 ;-2 ;-1)$ thuộc mặt phẳng $(P)$.
Cách 2:
Xét bài toán tổng quát: Cho hai đường thẳng $\Delta_1, \Delta_2$ phân biệt và không song song với nhau. Viết phương trình mặt phẳng $(P)$ chứa đường thẳng $\Delta_1$ và tạo với $\Delta_2$ một góc lớn nhất.
Phuơng pháp giải:
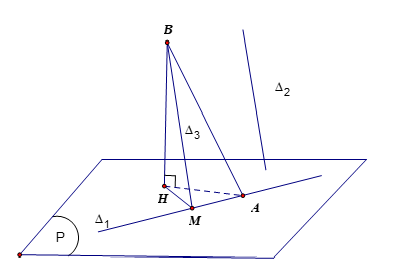+) Vẽ một đường thẳng $\Delta_3$ bất kỳ song song với $\Delta_2$ và cắt $\Delta_1$ tại $M$. Gọi $B$ là điểm cố định trên $\Delta_3$ và $H$ là hình chiếu vuông góc của $B$ lên $m p(P)$, kẻ $B A \perp \Delta_1$
$+)\left(\widehat{\Delta_2,(P)}\right)=\widehat{B M H}$
$\sin \widehat{B M H}=\dfrac{H B}{B M} \leq \dfrac{B A}{B M}$ không đổi
Suy ra $\widehat{B M H}$ lớn nhất khi $H \equiv A$
Khi đó $\widehat{B M H}=\left(\widehat{\Delta_1, \Delta_2}\right)$ và $(P)$ chứa $\Delta_1$ và vuông góc với mặt phẳng $\left(\Delta_1, \Delta_2\right)$.
Vậy $(P)$ có VTPT là: $\left[\left[\overrightarrow{u_{\Delta_1}}, \overrightarrow{u_{\Delta_2}}\right], \overrightarrow{u_{\Delta_1}}\right]$
Áp dung:
$\overrightarrow{u_d}=(1 ;-1 ;-2) ; \vec{j}=(0 ; 1 ; 0), \vec{n}=\left[\left[\overrightarrow{u_d}, \vec{\jmath}\right], \overrightarrow{u_d}\right]=(1 ; 5 ;-2)$. Phương trình mặt phẳng $(P)$ qua điểm $M(1 ;-2 ; 0)$, có véc tơ pháp tuyến $\vec{n}=(1 ; 5 ;-2)$ là $x+5 y-2 z+9=0$
Vậy điểm $N(-1 ;-2 ;-1)$ thuộc mặt phẳng $(P)$.