Tìm tham số $m$ để tồn tại duy nhất cặp số $(x ; y)$ thỏa mãn đồng...

Từ giả thiết, ta có $\left\{\begin{array}{l}0<x+y \leq 1(1) \\ x+y+\sqrt{2 x y+m} \geq 1(2)\end{array}\right.$.
Điều kiện cần.
Giả sử tồn tại cặp số $\left(x_0 ; y_0\right)$ thỏa mãn điều kiện (1) và (2), thì cặp số $\left(y_0 ; x_0\right)$ cũng thỏa điều kiện.
Do đó, để tồn tại cặp số $\left(x_0 ; y_0\right)$ duy nhất suy ra $x_0=y_0$. Ta có $\left\{\begin{array}{l}0<x_0 \leq \dfrac{1}{2}(3) \\ 2 x_0+\sqrt{2 x_0^2+m} \geq 1(4)\end{array}\right.$.
Do (3), ta có
(4) $\Leftrightarrow \sqrt{2 x_0^2+m} \geq 1-2 x_0 \Leftrightarrow 2 x_0^2+m \geq 1-4 x_0+4 x_0^2 \Leftrightarrow m \geq 2 x_0^2-4 x_0+1$ (5).
Xét hàm số $f(x)=2 x^2-4 x+1$ trên $\left(0 \dfrac{1}{2}\right]$, với bảng biến thiên như sau
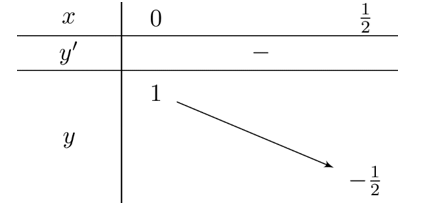Để bất phương trình (5) có nghiệm duy nhất $\Leftrightarrow m=-\dfrac{1}{2}$. Điều kiện đủ.
Với $m=-\dfrac{1}{2}$, hệ (1), (2) trở thành $\left\{\begin{array}{l}0<x+y \leq 1(6) \\ x+y+\sqrt{2 x y-\dfrac{1}{2}} \geq 1(7)\end{array}\right.$.
Do điều kiện (6), ta có
$
\begin{aligned}
& \text { (7) } \Leftrightarrow \sqrt{2 x y-\dfrac{1}{2}} \geq 1-(x+y) \\
& \Leftrightarrow 2 x y-\dfrac{1}{2} \geq 1-2(x+y)+x^2+2 x y+y^2 \\
& \Leftrightarrow x^2+y^2-2 x-2 y+\dfrac{3}{2} \leq 0 \\
& \Leftrightarrow\left(x-\dfrac{1}{2}\right)^2+\left(y-\dfrac{1}{2}\right)^2+(1-(x+y)) \leq 0 .
\end{aligned}
$
Dấu " = " xảy ra khi và chỉ khi $x=y=\dfrac{1}{2}$.Vậy $m=-\dfrac{1}{2}$ thỏa yêu cầu đề bài.