Câu hỏi: Một người thợ có một khối đá hình trụ. Kẻ hai đường kính MN, PQ của hai đáy sao cho $MN\bot PQ.$ Người thợ đó cắt khối đá theo các mặt cắt đi qua 3 trong 4 điểm M, N, P, Q để thu được khối đá có hình tứ diện MNPQ. Biết rằng MN = 60 cm và thể tích khối tứ diện MNPQ bằng $36d{{m}^{3}}.$ Tìm thể tích của lượng đá bị cắt bỏ (làm tròn kết quả đến 1 chữ số thập phân).
A. $133,6d{{m}^{3}}$
B. 113,6 $d{{m}^{3}}$
C. 143,6 $d{{m}^{3}}$
D. 123,6 $d{{m}^{3}}$
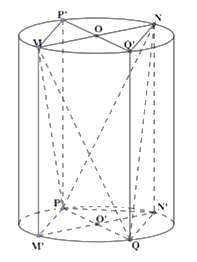
Dựng hình lăng trụ MP'NQ'.M'PN'Q (như hình vẽ)
Khi đó, ta có: ${{V}_{MNPQ}}={{V}_{MP'NQ'.M'PN'Q}}-\left( {{V}_{P.MNP'}}+{{V}_{Q.MNQ'}}+{{V}_{M.M'PQ}}+{{V}_{N.N'PQ}} \right)={{V}_{MP'NQ'.N'PN'Q}}-4.{{V}_{P.MNP'}}$
$\begin{aligned}
& ={{V}_{MP'NQ'.PN'Q}}-4.\dfrac{1}{2}{{V}_{P.MQ'NP'}}={{V}_{MP'NQ'.M'PN'Q}}-2{{V}_{P.MQ'NP'}} \\
& ={{V}_{MP'NQ'.PN'Q}}-2.\dfrac{1}{3}{{V}_{MP'NQ'.PN'Q}} \\
& =\dfrac{1}{3}{{V}_{MP'NQ'.PN'Q}}. \\
\end{aligned}$
$\Rightarrow \dfrac{1}{3}{{V}_{MP'NQ'.PN'Q}}=36(d{{m}^{3}})\Leftrightarrow {{V}_{MP'NQ'.PN'Q}}=108\left( d{{m}^{3}} \right)$
Do $MN\bot PQ,PQ//P'Q'$ nên $MN\bot P'Q'\Rightarrow MP'NQ'$ là hình vuông
Ta có: $MN=60cm\Rightarrow \left\{ \begin{aligned}
& MQ=\dfrac{60}{\sqrt{2}}=30\sqrt{2}(cm)=3\sqrt{2}(dm) \\
& OM=\dfrac{60}{2}=30(cm)=3(dm) \\
\end{aligned} \right.$
$\Rightarrow {{S}_{MP'NQ'}}={{\left( 3\sqrt{2} \right)}^{2}}=18(d{{m}^{2}})$
${{V}_{MP'NQ'.PN'Q}}={{S}_{MP'NQ'}}.h\Rightarrow 18h=108\Leftrightarrow h=6(dm)$
Thể tích khối trụ là: $V=\pi {{R}^{2}}h=\pi .O{{M}^{2}}h=\pi {{.3}^{2}}.6=54\pi (d{{m}^{3}})$
Thể tích của lượng đá bị cắt bỏ là: $54\pi -36\approx 133,6\left( d{{m}^{3}} \right).$
A. $133,6d{{m}^{3}}$
B. 113,6 $d{{m}^{3}}$
C. 143,6 $d{{m}^{3}}$
D. 123,6 $d{{m}^{3}}$
Dựng hình lăng trụ MP'NQ'.M'PN'Q (như hình vẽ)
Khi đó, ta có: ${{V}_{MNPQ}}={{V}_{MP'NQ'.M'PN'Q}}-\left( {{V}_{P.MNP'}}+{{V}_{Q.MNQ'}}+{{V}_{M.M'PQ}}+{{V}_{N.N'PQ}} \right)={{V}_{MP'NQ'.N'PN'Q}}-4.{{V}_{P.MNP'}}$
$\begin{aligned}
& ={{V}_{MP'NQ'.PN'Q}}-4.\dfrac{1}{2}{{V}_{P.MQ'NP'}}={{V}_{MP'NQ'.M'PN'Q}}-2{{V}_{P.MQ'NP'}} \\
& ={{V}_{MP'NQ'.PN'Q}}-2.\dfrac{1}{3}{{V}_{MP'NQ'.PN'Q}} \\
& =\dfrac{1}{3}{{V}_{MP'NQ'.PN'Q}}. \\
\end{aligned}$
$\Rightarrow \dfrac{1}{3}{{V}_{MP'NQ'.PN'Q}}=36(d{{m}^{3}})\Leftrightarrow {{V}_{MP'NQ'.PN'Q}}=108\left( d{{m}^{3}} \right)$
Do $MN\bot PQ,PQ//P'Q'$ nên $MN\bot P'Q'\Rightarrow MP'NQ'$ là hình vuông
Ta có: $MN=60cm\Rightarrow \left\{ \begin{aligned}
& MQ=\dfrac{60}{\sqrt{2}}=30\sqrt{2}(cm)=3\sqrt{2}(dm) \\
& OM=\dfrac{60}{2}=30(cm)=3(dm) \\
\end{aligned} \right.$
$\Rightarrow {{S}_{MP'NQ'}}={{\left( 3\sqrt{2} \right)}^{2}}=18(d{{m}^{2}})$
${{V}_{MP'NQ'.PN'Q}}={{S}_{MP'NQ'}}.h\Rightarrow 18h=108\Leftrightarrow h=6(dm)$
Thể tích khối trụ là: $V=\pi {{R}^{2}}h=\pi .O{{M}^{2}}h=\pi {{.3}^{2}}.6=54\pi (d{{m}^{3}})$
Thể tích của lượng đá bị cắt bỏ là: $54\pi -36\approx 133,6\left( d{{m}^{3}} \right).$
Đáp án A.