Gọi $m_o$ là giá trị nhỏ nhất của tham số thực $m$ sao cho phương...

Phương trình đã cho trở thành
$
\begin{aligned}
& (\mathrm{m}-1) \log _{\dfrac{1}{2}}^2(x-2)-(\mathrm{m}-5) \log _{\dfrac{1}{2}}(x-2)+\mathrm{m}-1=0 \\
& \Leftrightarrow(\mathrm{m}-1) \log _2^2(x-2)+(\mathrm{m}-5) \log _2(x-2)+(\mathrm{m}-1)=0(1) \\
& \text { Đặt } \log _2(x-2)=\mathrm{t} \Rightarrow \mathrm{t}<1 \\
& \Leftrightarrow m\left(t^2+t+1\right)=t^2+5 t+1 \\
& \text { Khi đó } m=\dfrac{t^2+5 t+1}{t^2+t+1}=1+\dfrac{4 t}{t^2+t+1} \\
& \text { Xét hàm sô } f(t)=1+\dfrac{4 t}{t^2+t+1} \text { trên }(-\infty ; 1) \\
& \text { Ta có } f^{\prime}(t)=\dfrac{4\left(1-t^2\right)}{\left(t^2+t+1\right)^2}=0 \Leftrightarrow t= \pm 1
\end{aligned}
$
Ta có $f^{\prime}(t)=\dfrac{4\left(1-t^2\right)}{\left(t^2+t+1\right)^2}=0 \Leftrightarrow t= \pm 1$
Ta có BBT:
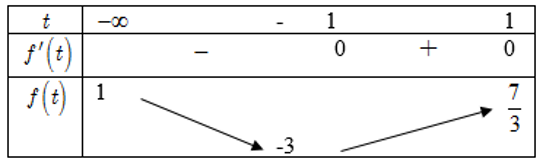Dựa vào $\mathrm{BBT}$, suy ra $-3 \leq m<\dfrac{7}{3}$. Suy ra, GTNN của $m$ là $m=-3$.