Có bao nhiêu giá trị nguyên của tham số $m(|m|<2020)$ để phương...

Điều kiện: $x+2m>0$
Ta có ${{2}^{x-1}}={{\log }_{4}}\left( x+2m \right)+m\Leftrightarrow {{2}^{x}}={{\log }_{2}}\left( x+2m \right)+2m$
Đặt $t={{\log }_{2}}\left( x+2m \right)taco\left\{ \begin{aligned}
& {{2}^{x}}=t+2m \\
& {{2}^{t}}=x+2m \\
\end{aligned} \right.\Rightarrow {{2}^{x}}+x={{2}^{t}}+t\left( 1 \right)$

Xét hàm số $f\left( u \right)={{2}^{u}}+u$ ta có $f'\left( u \right)={{2}^{u}}\ln 2+1>0\forall u\in R$ do đó $f\left( u \right)$ đồng biến trên R, nên ta có (1) $\Leftrightarrow f\left( x \right)=f\left( t \right)\Leftrightarrow x=t$
Khi đó: ${{2}^{x}}=x+2m\Leftrightarrow {{2}^{x}}-x=2m$
Xét hàm số $g\left( x \right)={{2}^{x}}-x\Rightarrow g'\left( x \right)={{2}^{x}}\ln 2-1=0\Leftrightarrow x=-{{\log }_{2}}\left( \ln 2 \right)$
Bảng biến thiên:
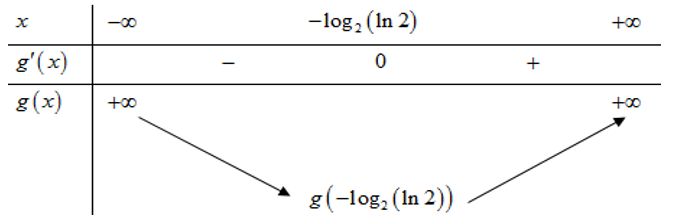Từ đó phương trình đã cho có nghiệm khi và chỉ khi $2 m \geq g\left(-\log _2(\ln 2)\right)$ $\Leftrightarrow m \geq \dfrac{g\left(-\log _2(\ln 2)\right)}{2}=\dfrac{(\ln 2)^{-1}+\log _2(\ln 2)}{2} \approx 0.457$ (các nghiệm này đều thỏa mãn điều kiện vì $x+$ $\left.2 m=2^x>0\right)$
Do $m$ nguyên và $|m|<2020$, nên $m \in\{1,2,3, \ldots, 2019\}$.