Có bao nhiêu giá trị nguyên của tham số $m$ thuộc đoạn $\left[...

Điều kiện: $x>-1$.
Phương trình $\Leftrightarrow x{{\log }_{2}}\left( x+1 \right)={{\log }_{4}}16+{{\log }_{4}}\left[ {{\left( x+1 \right)}^{2m}} \right]$ $\Leftrightarrow x{{\log }_{2}}\left( x+1 \right)=2+m{{\log }_{2}}\left( x+1 \right)$.
Đặt $t={{\log }_{2}}\left( x+1 \right),t\in {R}\Rightarrow x={{2}^{t}}-1$. Khi đó ta có phương trình $\Leftrightarrow \left( {{2}^{t}}-1 \right)t=2+mt$ (1)
+ Nếu $t=0$ thì không thoả mãn phương trình (1)
+ Nếu $t\ne 0$ thì (1) $\Leftrightarrow m={{2}^{t}}-1-\dfrac{2}{t}$ (2).
Đặt $f\left( t \right)={{2}^{t}}-1-\dfrac{2}{t};t\ne 0$. $\Rightarrow {f}'\left( t \right)={{2}^{t}}.\ln 2+\dfrac{2}{{{t}^{2}}}>0,\forall t\ne 0$. Ta có bảng biến thiên
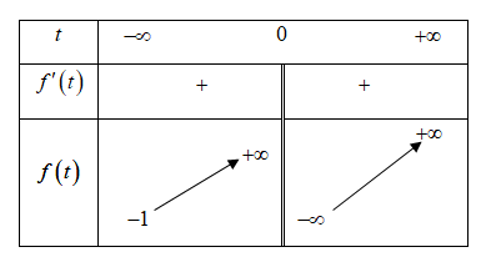Với $\underset{t\to +\infty }{\mathop{\lim }} f\left( t \right)=+\infty $, $\underset{t\to -\infty }{\mathop{\lim }} f\left( t \right)=-1$, $\underset{t\to {{0}^{+}}}{\mathop{\lim }} f\left( t \right)=-\infty $, $\underset{t\to {{0}^{-}}}{\mathop{\lim }} f\left( t \right)=+\infty $.
Phương trình đã cho có 2 nghiệm $\Leftrightarrow \left( 2 \right)$ có 2 nghiệm phân biệt $t\ne 0$ $\Leftrightarrow m>-1$.
Vì $m\in \mathbb{Z}$ và $m\in \left[ -2022; 2023 \right]$ nên $m\in \left\{ 0; 1; 2; ...; 2023 \right\}$. Vậy có 2024 số nguyên $m$.