Có bao nhiêu giá trị nguyên của tham số $m\in \left[ -2023;2023...

Xét phương trình $\left( {{x}^{2}}-1 \right){{\log }^{2}}\left( {{x}^{2}}+1 \right)-m\sqrt{2\left( {{x}^{2}}-1 \right)}\log \left( {{x}^{2}}+1 \right)+m+4=0\quad \left( * \right)$.
Dễ thấy rằng nếu phương trình có nghiệm là ${{x}_{0}}$ thì phương trình cũng có nghiệm là $-{{x}_{0}}$.
Đặt $t={{x}^{2}}$, ta được phương trình $\left( t-1 \right){{\log }^{2}}\left( t+1 \right)-m\sqrt{2\left( t-1 \right)}\log \left( t+1 \right)+m+4=0\quad \left( 1 \right)$.
Để $\left( * \right)$ có hai nghiệm ${{x}_{1}},\ {{x}_{2}}$ thỏa mãn $1\le \left| {{x}_{1}} \right|\le \left| {{x}_{2}} \right|\le 3$ thì $\left( 1 \right)$ có đúng một nghiệm $t$ thỏa mãn $1\le t\le 9$.
Đặt $u=\sqrt{2\left( t-1 \right)}\log \left( t+1 \right)$.
Ta có ${u}'=\dfrac{1}{\sqrt{2\left( t-1 \right)}}\log \left( t+1 \right)+\sqrt{2\left( t-1 \right)}.\dfrac{1}{t+1}>0,\ \forall t\in \left( 1;9 \right]$.
Nên $u$ đồng biến trên $\left( 1;9 \right]$ $\Rightarrow 0\le u\le 4$.
Để $\left( 1 \right)$ có đúng một nghiệm $t$ thỏa mãn $1\le t\le 9$ thì phương trình ${{u}^{2}}-2mu+2m+8=0\quad \left( 2 \right)$ có đúng một nghiệm $u$ thỏa mãn $0\le u\le 4$.
Ta có ${{u}^{2}}-2mu+2m+8=0\Leftrightarrow 2m=\dfrac{{{u}^{2}}+8}{u-1}=u+1+\dfrac{9}{u-1}$ (do $u=1$ không thỏa mãn $\left( 2 \right)$ )
Xét hàm số $f\left( u \right)=u+1+\dfrac{9}{u-1}$, ta có ${f}'\left( u \right)=1-\dfrac{9}{{{\left( u-1 \right)}^{2}}}=\dfrac{\left( u+2 \right)\left( u-4 \right)}{{{\left( u-1 \right)}^{2}}}\le 0,\forall u\in \left[ 0;4 \right]\backslash \left\{ 1 \right\}$.
Bảng biến thiên:
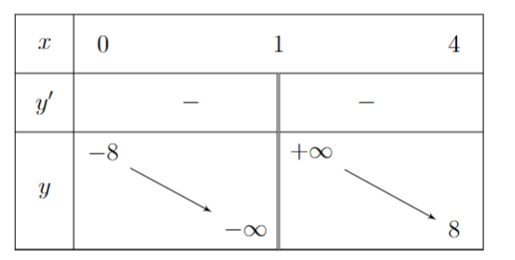Phương trình ${{u}^{2}}-2mu+2m+8=0$ có đúng một nghiệm $u$ thỏa mãn $0\le u\le 4$ khi và chỉ khi $\left[ \begin{matrix}
2m\ge 8 \\
2m\le -8 \\
\end{matrix} \right.\Leftrightarrow \left[ \begin{matrix}
m\ge 4 \\
m\le -4 \\
\end{matrix} \right.$.
Do $m\in \left[ -2023;2023 \right]\cap \mathbb{Z}$ nên $m\in \left\{ -2023;\ -2022;\ ...;\ -4;\ 4;\ 5;\ ...;\ 2023 \right\}$.
Vậy có tất cả $4040$ giá trị $m$.