Google
Câu hỏi: Cho tứ diện $ABCD$ có tam giác $BCD$ vuông tại $C$, $AB$ vuông góc với mặt phẳng $\left( BCD \right)$, $AB=5a , BC=3a$ và $CD=4a$. Tính bán kính $R$ của mặt cầu ngoại tiếp tứ diện $ABCD$.
A. $R=\dfrac{5a\sqrt{2}}{3}$.
B. $R=\dfrac{5a\sqrt{3}}{3}$.
C. $R=\dfrac{5a\sqrt{2}}{2}$.
D. $R=\dfrac{5a\sqrt{3}}{2}$.
A. $R=\dfrac{5a\sqrt{2}}{3}$.
B. $R=\dfrac{5a\sqrt{3}}{3}$.
C. $R=\dfrac{5a\sqrt{2}}{2}$.
D. $R=\dfrac{5a\sqrt{3}}{2}$.
Cách 1 áp dụng công thức tính nhanh ${{R}_{c}}=\sqrt{{{\left( {{R}_{d}} \right)}^{2}}+\dfrac{h{}^{2}}{4}}$
Trong đó bán kính của đường tròn ngoại tiếp tam giác $BCD$ bằng ${{R}_{d}}=\dfrac{BD}{2}=\dfrac{\sqrt{B{{C}^{2}}+C{{D}^{2}}}}{2}=\dfrac{\sqrt{{{\left( 3a \right)}^{2}}+{{\left( 4a \right)}^{2}}}}{2}=\dfrac{5a}{2}$.
Chiều cao của tứ diện $h=AB=5a$.
Vậy ${{R}_{c}}=\sqrt{{{\left( \dfrac{5a}{2} \right)}^{2}}+\dfrac{\left( 5a \right){}^{2}}{4}}=\dfrac{5a\sqrt{2}}{2}$.
Cách 2
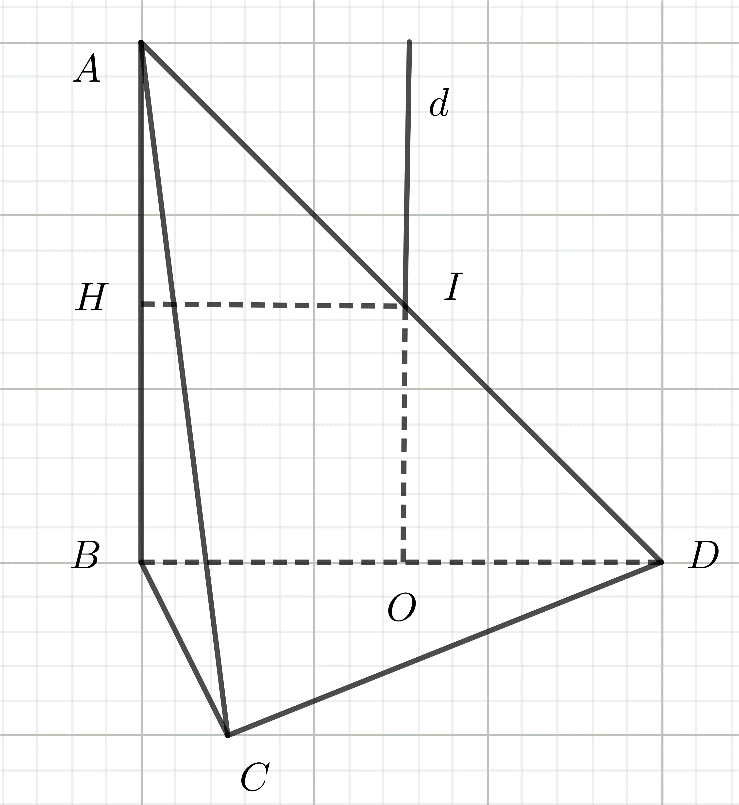Do tam giác $BCD$ vuông tại $C$ nên gọi $O$ là tâm đường tròn ngoại tiếp tam giác $BCD$ $\Rightarrow O$ là trung điểm $BC$ .
Dựng trục $d$ của đường tròn ngoại tiếp tam giác $BCD$.
Dựng mặt phẳng $\left( P \right)$ là mặt phẳng trung trực của cạnh $AB$ cắt $AB$ tại $H$.
Giả sử $d\cap \left( P \right)=I$ .
Ta có $I\in d\Rightarrow IB=IC=ID \left( 1 \right)$.
Lại có $I\in \left( P \right)\Rightarrow IA=IB \left( 2 \right)$.
Từ $\left( 1 \right)$ và $\left( 2 \right)$ ta có $IA=IB=IC=ID$ $\Rightarrow I$ chính là tâm mặt cầu ngoại tiếp tứ diện và bán kính
$R=\sqrt{{{\left( HB \right)}^{2}}+{{\left( OB \right)}^{2}}}=\sqrt{{{\left( \dfrac{5a}{2} \right)}^{2}}+{{\left( \dfrac{5a}{2} \right)}^{2}}}=\dfrac{5a\sqrt{2}}{2}$.
Trong đó bán kính của đường tròn ngoại tiếp tam giác $BCD$ bằng ${{R}_{d}}=\dfrac{BD}{2}=\dfrac{\sqrt{B{{C}^{2}}+C{{D}^{2}}}}{2}=\dfrac{\sqrt{{{\left( 3a \right)}^{2}}+{{\left( 4a \right)}^{2}}}}{2}=\dfrac{5a}{2}$.
Chiều cao của tứ diện $h=AB=5a$.
Vậy ${{R}_{c}}=\sqrt{{{\left( \dfrac{5a}{2} \right)}^{2}}+\dfrac{\left( 5a \right){}^{2}}{4}}=\dfrac{5a\sqrt{2}}{2}$.
Cách 2
Dựng trục $d$ của đường tròn ngoại tiếp tam giác $BCD$.
Dựng mặt phẳng $\left( P \right)$ là mặt phẳng trung trực của cạnh $AB$ cắt $AB$ tại $H$.
Giả sử $d\cap \left( P \right)=I$ .
Ta có $I\in d\Rightarrow IB=IC=ID \left( 1 \right)$.
Lại có $I\in \left( P \right)\Rightarrow IA=IB \left( 2 \right)$.
Từ $\left( 1 \right)$ và $\left( 2 \right)$ ta có $IA=IB=IC=ID$ $\Rightarrow I$ chính là tâm mặt cầu ngoại tiếp tứ diện và bán kính
$R=\sqrt{{{\left( HB \right)}^{2}}+{{\left( OB \right)}^{2}}}=\sqrt{{{\left( \dfrac{5a}{2} \right)}^{2}}+{{\left( \dfrac{5a}{2} \right)}^{2}}}=\dfrac{5a\sqrt{2}}{2}$.
Đáp án C.