Google
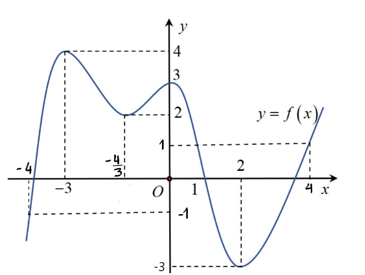
Câu hỏi: Cho số $y=f\left( x \right)$ là hàm số bậc 5 có đạo hàm liên tục trên $\mathbb{R}$ và có đúng 4 điểm cực trị trên là $-3; -\dfrac{4}{3}; 0 ; 2$ và có đồ thị như hình vẽ.
Có bao nhiêu giá trị nguyên của tham số $m\in \left[ -2023;2023 \right]$ để hàm số $y=\left| f({{x}^{3}}+3x)+m \right|$ nghịch biến trên $\left( -4;-1 \right)$ ?
A. $2025$.
B. $2024$.
C. $2023$.
D. $2022$
A. $2025$.
B. $2024$.
C. $2023$.
D. $2022$
Đặt $t={{x}^{3}}+3x$ $\Rightarrow t'=3{{x}^{2}}+3>0$, do đó với $x\in \left( -4;-1 \right)\Rightarrow t\in \left( -76;-4 \right)$
Xét hàm số $g\left( t \right)=f\left( t \right)+m$, $g'\left( t \right)=f'\left( t \right)>0\forall t\in \left( -76;-4 \right)$
Do đó yêu cầu của bài toán $\Rightarrow h\left( -4 \right)\le 0\Rightarrow f\left( -4 \right)+m\le 0\Rightarrow -1+m\le 0\Rightarrow m\le 1$
Do $m\in \mathbb{Z}, m\in \left[ -2023;2023 \right]$ nên $m\in \left\{ -2023;...;1 \right\}$, có $2025$ giá trị $m$ thỏa mãn.
Xét hàm số $g\left( t \right)=f\left( t \right)+m$, $g'\left( t \right)=f'\left( t \right)>0\forall t\in \left( -76;-4 \right)$
Do đó yêu cầu của bài toán $\Rightarrow h\left( -4 \right)\le 0\Rightarrow f\left( -4 \right)+m\le 0\Rightarrow -1+m\le 0\Rightarrow m\le 1$
Do $m\in \mathbb{Z}, m\in \left[ -2023;2023 \right]$ nên $m\in \left\{ -2023;...;1 \right\}$, có $2025$ giá trị $m$ thỏa mãn.
Đáp án A.
