Google
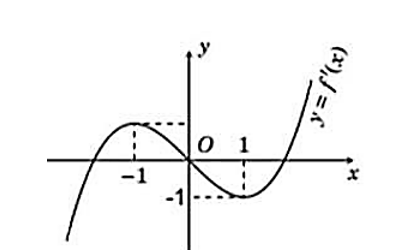
Câu hỏi: Cho hàm số $y=f\left( x \right)$ liên tục và có đạo hàm trên $\mathbb{R}$, $f\left( 0 \right)=3$ và đồ thị hàm số $y={f}'\left( x \right)$ như hình vẽ.
Có bao nhiêu giá trị nguyên $m$ để hàm số $g\left( x \right)=\left| 2f\left( x \right)+{{x}^{2}}-2mx+2m \right|$ đồng biến trên $\left( 0;1 \right)$ ?
A. $2$.
B. $1$.
C. $4$.
D. $3$.
A. $2$.
B. $1$.
C. $4$.
D. $3$.
Đặt $h\left( x \right)=2f\left( x \right)+{{x}^{2}}-2mx+2m\Rightarrow {h}'\left( x \right)=2{f}'\left( x \right)+2x-2m.$
Chọn hàm ${{f}'}'\left( x \right)=3a\left( {{x}^{2}}-1 \right)\Rightarrow {f}'\left( x \right)=a\left( {{x}^{3}}-3x \right)+d$.
$\left\{ \begin{aligned}
& {f}'\left( 0 \right)=0 \\
& {f}'\left( 1 \right)=-1 \\
\end{aligned} \right.\Rightarrow \left\{ \begin{aligned}
& d=0 \\
& a=\dfrac{1}{2} \\
\end{aligned} \right.\Rightarrow {f}'\left( x \right)=\dfrac{{{x}^{3}}-3x}{2}$.
Xét hàm $p\left( x \right)={f}'\left( x \right)+x=\dfrac{{{x}^{3}}-x}{2}, x\in \left( 0;1 \right)$.
${p}'\left( x \right)=\dfrac{3{{x}^{2}}-1}{2}=0\Leftrightarrow \left[ \begin{aligned}
& x=1/\sqrt{3} \left( t/m \right) \\
& x=-1/\sqrt{3} \left( l \right) \\
\end{aligned} \right.$.
Ta có bảng biến thiên:
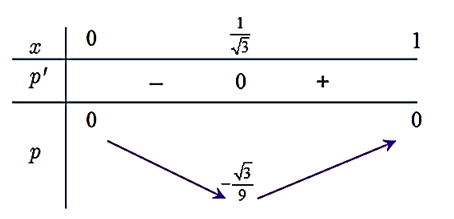Như vậy: $-\dfrac{\sqrt{3}}{9}\le p\left( x \right)<0, \forall x\in \left( 0;1 \right)$.
Hàm số $g\left( x \right)=\left| 2f\left( x \right)+{{x}^{2}}-2mx+2m \right|$ đồng biến trên $\left( 0;1 \right)$ khi và chỉ khi xảy ra một trong hai trường hợp sau:
TH1: $\left\{ \begin{aligned}
& h\left( 0 \right)=6+2m\ge 0 \\
& {h}'\left( x \right)\ge 0 , \forall x\in \left( 0;1 \right) \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& m\ge -3 \\
& m\le {f}'\left( x \right)+x , \forall x\in \left( 0;1 \right) \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& m\ge -3 \\
& m\le -\dfrac{\sqrt{3}}{9} \\
\end{aligned} \right.$.
Vì $m\in \mathbb{Z}$ nên $m\in \left\{ -3;-2;-1 \right\}$.
TH2: $\left\{ \begin{aligned}
& h\left( 0 \right)=6+2m\le 0 \\
& {h}'\left( x \right)\le 0 , \forall x\in \left( 0;1 \right) \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& m\le -3 \\
& m\ge {f}'\left( x \right)+x , \forall x\in \left( 0;1 \right) \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& m\le -3 \\
& m\ge 0 \\
\end{aligned} \right.$ (loại).
Vậy $m\in \left\{ -3;-2;-1 \right\}$.
Chọn hàm ${{f}'}'\left( x \right)=3a\left( {{x}^{2}}-1 \right)\Rightarrow {f}'\left( x \right)=a\left( {{x}^{3}}-3x \right)+d$.
$\left\{ \begin{aligned}
& {f}'\left( 0 \right)=0 \\
& {f}'\left( 1 \right)=-1 \\
\end{aligned} \right.\Rightarrow \left\{ \begin{aligned}
& d=0 \\
& a=\dfrac{1}{2} \\
\end{aligned} \right.\Rightarrow {f}'\left( x \right)=\dfrac{{{x}^{3}}-3x}{2}$.
Xét hàm $p\left( x \right)={f}'\left( x \right)+x=\dfrac{{{x}^{3}}-x}{2}, x\in \left( 0;1 \right)$.
${p}'\left( x \right)=\dfrac{3{{x}^{2}}-1}{2}=0\Leftrightarrow \left[ \begin{aligned}
& x=1/\sqrt{3} \left( t/m \right) \\
& x=-1/\sqrt{3} \left( l \right) \\
\end{aligned} \right.$.
Ta có bảng biến thiên:
Hàm số $g\left( x \right)=\left| 2f\left( x \right)+{{x}^{2}}-2mx+2m \right|$ đồng biến trên $\left( 0;1 \right)$ khi và chỉ khi xảy ra một trong hai trường hợp sau:
TH1: $\left\{ \begin{aligned}
& h\left( 0 \right)=6+2m\ge 0 \\
& {h}'\left( x \right)\ge 0 , \forall x\in \left( 0;1 \right) \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& m\ge -3 \\
& m\le {f}'\left( x \right)+x , \forall x\in \left( 0;1 \right) \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& m\ge -3 \\
& m\le -\dfrac{\sqrt{3}}{9} \\
\end{aligned} \right.$.
Vì $m\in \mathbb{Z}$ nên $m\in \left\{ -3;-2;-1 \right\}$.
TH2: $\left\{ \begin{aligned}
& h\left( 0 \right)=6+2m\le 0 \\
& {h}'\left( x \right)\le 0 , \forall x\in \left( 0;1 \right) \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& m\le -3 \\
& m\ge {f}'\left( x \right)+x , \forall x\in \left( 0;1 \right) \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& m\le -3 \\
& m\ge 0 \\
\end{aligned} \right.$ (loại).
Vậy $m\in \left\{ -3;-2;-1 \right\}$.
Đáp án D.
