Google
Câu hỏi: Cho hàm số $y=f\left( x \right)$ có đạo hàm trên $\mathbb{R}$ và $f\left( 1 \right)=1$. Hàm số $y={f}'\left( x \right)$ có đồ thị là đường cong như hình bên dưới.
Có bao nhiêu số nguyên dương $a$ để hàm số $g\left( x \right)=\left| 4f\left( \sin x \right)+\cos 2x-a \right|$ nghịch biến trên khoảng $\left( 0; \dfrac{\pi }{2} \right)$ ?
A. $4$.
B. $5$.
C. $2$.
D. $3$.
A. $4$.
B. $5$.
C. $2$.
D. $3$.
Ta có: $g\left( x \right)=\left| 4f\left( \sin x \right)+\cos 2x-a \right|=\left| 4f\left( \sin x \right)+1-2{{\sin }^{2}}x-a \right|$.
Đặt $t=\sin x, x\in \left( 0; \dfrac{\pi }{2} \right)\Rightarrow t\in \left( 0; 1 \right)$ và ta có hàm số $y=\sin x$ đồng biến trên khoảng $\left( 0; \dfrac{\pi }{2} \right)$.
Xét hàm số $g\left( t \right)=4f\left( t \right)-2{{t}^{2}}+1-a\to {g}'\left( t \right)=4{f}'\left( t \right)-4t$ trên khoảng $\left( 0; 1 \right)$.
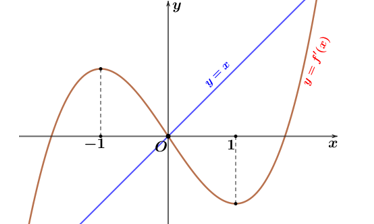Ta có: $g\left( 1 \right)=4f\left( 1 \right)-1-a=3-a$ và từ đồ thị ta suy ra ${f}'\left( x \right)<x, \forall x\in \left( 0;1 \right)$ (đúng).
Điều kiện bài toán $\Leftrightarrow \left[ \begin{aligned}
& \left\{ \begin{aligned}
& {g}'\left( t \right)\le 0, \forall t\in \left( 0; 1 \right) \\
& g\left( 1 \right)\ge 0 \\
\end{aligned} \right.\Rightarrow a\le 3 \\
& \left\{ \begin{aligned}
& {g}'\left( t \right)\ge 0, \forall t\in \left( 0; 1 \right) \\
& g\left( 1 \right)\le 0 \\
\end{aligned} \right. \left( loai \right) \\
\end{aligned} \right.$.
Vì $a$ nguyên dương nên $a\in \left\{ 1; 2; 3 \right\}$.
Đặt $t=\sin x, x\in \left( 0; \dfrac{\pi }{2} \right)\Rightarrow t\in \left( 0; 1 \right)$ và ta có hàm số $y=\sin x$ đồng biến trên khoảng $\left( 0; \dfrac{\pi }{2} \right)$.
Xét hàm số $g\left( t \right)=4f\left( t \right)-2{{t}^{2}}+1-a\to {g}'\left( t \right)=4{f}'\left( t \right)-4t$ trên khoảng $\left( 0; 1 \right)$.
Điều kiện bài toán $\Leftrightarrow \left[ \begin{aligned}
& \left\{ \begin{aligned}
& {g}'\left( t \right)\le 0, \forall t\in \left( 0; 1 \right) \\
& g\left( 1 \right)\ge 0 \\
\end{aligned} \right.\Rightarrow a\le 3 \\
& \left\{ \begin{aligned}
& {g}'\left( t \right)\ge 0, \forall t\in \left( 0; 1 \right) \\
& g\left( 1 \right)\le 0 \\
\end{aligned} \right. \left( loai \right) \\
\end{aligned} \right.$.
Vì $a$ nguyên dương nên $a\in \left\{ 1; 2; 3 \right\}$.
Đáp án D.