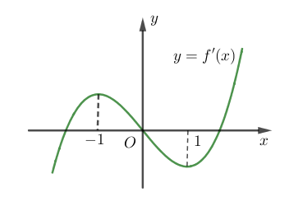
Câu hỏi: Cho hàm số $f(x)$ có đạo hàm trên $\mathbb{R}$ và $f(1)=1$. Đồ thị hàm số $y=f^{\prime}(x)$ như hình bên. Có bao nhiêu số nguyên dương $a$ để hàm số $y=|4 f(\sin x)+\cos 2 x-a|$ nghịch biến trên $\left(0 ; \dfrac{\pi}{2}\right)$ ?
A. 5 .
B. 2 .
C. 3 .
D. Vô số.
A. 5 .
B. 2 .
C. 3 .
D. Vô số.
Đặt $g(x)=|4 f(\sin x)+\cos 2 x-a| \Rightarrow g(x)=\sqrt{[4 f(\sin x)+\cos 2 x-a]^2}$.
$\Rightarrow g^{\prime}(x)=\dfrac{\left[4 \cos x \cdot f^{\prime}(\sin x)-2 \sin 2 x\right][4 f(\sin x)+\cos 2 x-a]}{\sqrt{[4 f(\sin x)+\cos 2 x-a]^2}}$.
Ta có $4 \cos x . f^{\prime}(\sin x)-2 \sin 2 x=4 \cos x\left[f^{\prime}(\sin x)-\sin x\right]$.
Với $x \in\left(0 ; \dfrac{\pi}{2}\right)$ thì $\cos x>0, \sin x \in(0 ; 1) \Rightarrow f^{\prime}(\sin x)-\sin x<0$.
Hàm số $g(x)$ nghịch biến trên $\left(0 ; \dfrac{\pi}{2}\right)$ khi $4 f(\sin x)+\cos 2 x-a \geq 0, \forall x \in\left(0 ; \dfrac{\pi}{2}\right)$
$\Leftrightarrow 4 f(\sin x)+1-2 \sin ^2 x \geq a, \forall x \in\left(0 ; \dfrac{\pi}{2}\right)$.
Đặt $t=\sin x$ được $4 f(t)+1-2 t^2 \geq a, \forall t \in(0 ; 1)(*)$.
Xét $h(t)=4 f(t)+1-2 t^2 \Rightarrow h^{\prime}(t)=4 f^{\prime}(t)-4 t=4\left[f^{\prime}(t)-1\right]$.
Với $t \in(0 ; 1)$ thì $h^{\prime}(t)<0 \Rightarrow h(t)$ nghịch biến trên $(0 ; 1)$.
Do đó $\left(^*\right) \Leftrightarrow a \leq h(1)=4 f(1)+1-2.1^2=3$. Vậy có 3 giá trị nguyên dương của $a$ thỏa mãn.
$\Rightarrow g^{\prime}(x)=\dfrac{\left[4 \cos x \cdot f^{\prime}(\sin x)-2 \sin 2 x\right][4 f(\sin x)+\cos 2 x-a]}{\sqrt{[4 f(\sin x)+\cos 2 x-a]^2}}$.
Ta có $4 \cos x . f^{\prime}(\sin x)-2 \sin 2 x=4 \cos x\left[f^{\prime}(\sin x)-\sin x\right]$.
Với $x \in\left(0 ; \dfrac{\pi}{2}\right)$ thì $\cos x>0, \sin x \in(0 ; 1) \Rightarrow f^{\prime}(\sin x)-\sin x<0$.
Hàm số $g(x)$ nghịch biến trên $\left(0 ; \dfrac{\pi}{2}\right)$ khi $4 f(\sin x)+\cos 2 x-a \geq 0, \forall x \in\left(0 ; \dfrac{\pi}{2}\right)$
$\Leftrightarrow 4 f(\sin x)+1-2 \sin ^2 x \geq a, \forall x \in\left(0 ; \dfrac{\pi}{2}\right)$.
Đặt $t=\sin x$ được $4 f(t)+1-2 t^2 \geq a, \forall t \in(0 ; 1)(*)$.
Xét $h(t)=4 f(t)+1-2 t^2 \Rightarrow h^{\prime}(t)=4 f^{\prime}(t)-4 t=4\left[f^{\prime}(t)-1\right]$.
Với $t \in(0 ; 1)$ thì $h^{\prime}(t)<0 \Rightarrow h(t)$ nghịch biến trên $(0 ; 1)$.
Do đó $\left(^*\right) \Leftrightarrow a \leq h(1)=4 f(1)+1-2.1^2=3$. Vậy có 3 giá trị nguyên dương của $a$ thỏa mãn.
Đáp án C.