Google
Câu hỏi: Cho lăng trụ $ABC.{A}'{B}'{C}'$, có đáy $ABC$ là tam giác đều cạnh $a$. Cho biết hình chiếu của đỉnh ${A}'$ trên mặt đáy $\left( ABC \right)$ là điểm $H$ trên cạnh $AB$ mà $HA=2HB$ và góc giữa mặt bên $\left( {A}'{C}'CA \right)$ và mặt đáy $\left( ABC \right)$ bằng ${{45}^{0}}.$ Thể tích của khối lăng trụ đã cho bằng
A. $\dfrac{1}{4}{{a}^{3}}.$
B. $\dfrac{3}{4}{{a}^{3}}.$
C. $\dfrac{\sqrt{3}}{4}{{a}^{3}}.$
D. $\dfrac{1}{12}{{a}^{3}}.$
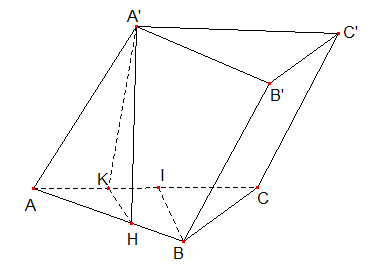Kẻ $HK\bot AC$
Ta có $A'H\bot \left( ABC \right)\Rightarrow A'H\bot AC$ $A'H\bot \left( ABC \right)\Rightarrow A'H\bot AC$
Từ và $AC\bot \left( A'HK \right)\Rightarrow AC\bot A'K$
Theo bài ra ta có góc giữa mặt bên $\left( {A}'{C}'CA \right)$ và mặt đáy $\left( ABC \right)$ bằng ${{45}^{0}}$ là góc giữa $HK$ và ${{A}^{'}}K$.
Hay góc $\widehat{A'KH}={{45}^{0}}$
Tam giác vuông ${{A}^{'}}HK$ có $\widehat{A'KH}={{45}^{0}}$ nên tam giác ${{A}^{'}}HK$ vuông cân tại $H$. Do đó: $HK={{A}^{'}}H$.
Gọi I là chân đường cao hạ từ B của tam giác ABC
Ta có: $\dfrac{AH}{AB}=\dfrac{HK}{BI}\Rightarrow HK=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\Rightarrow A'H=HK=\dfrac{a\sqrt{3}}{3}$ $$
Vậy: ${{V}_{ABC.A'B'C'}}={{S}_{\Delta ABC}}.A'H=\frac{{{a}^{2}}\sqrt{3}}{4}.\frac{a\sqrt{3}}{3}=\frac{{{a}^{3}}}{4}$.
A. $\dfrac{1}{4}{{a}^{3}}.$
B. $\dfrac{3}{4}{{a}^{3}}.$
C. $\dfrac{\sqrt{3}}{4}{{a}^{3}}.$
D. $\dfrac{1}{12}{{a}^{3}}.$
Ta có $A'H\bot \left( ABC \right)\Rightarrow A'H\bot AC$ $A'H\bot \left( ABC \right)\Rightarrow A'H\bot AC$
Từ và $AC\bot \left( A'HK \right)\Rightarrow AC\bot A'K$
Theo bài ra ta có góc giữa mặt bên $\left( {A}'{C}'CA \right)$ và mặt đáy $\left( ABC \right)$ bằng ${{45}^{0}}$ là góc giữa $HK$ và ${{A}^{'}}K$.
Hay góc $\widehat{A'KH}={{45}^{0}}$
Tam giác vuông ${{A}^{'}}HK$ có $\widehat{A'KH}={{45}^{0}}$ nên tam giác ${{A}^{'}}HK$ vuông cân tại $H$. Do đó: $HK={{A}^{'}}H$.
Gọi I là chân đường cao hạ từ B của tam giác ABC
Ta có: $\dfrac{AH}{AB}=\dfrac{HK}{BI}\Rightarrow HK=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\Rightarrow A'H=HK=\dfrac{a\sqrt{3}}{3}$ $$
Vậy: ${{V}_{ABC.A'B'C'}}={{S}_{\Delta ABC}}.A'H=\frac{{{a}^{2}}\sqrt{3}}{4}.\frac{a\sqrt{3}}{3}=\frac{{{a}^{3}}}{4}$.
Đáp án A.