Google
Câu hỏi: Cho hình trụ có hai đáy là hai đường tròn $\left( O \right)$ và $\left( {{O}'} \right)$ bán kính bằng $a\sqrt{3}$. Một khối nón có đỉnh $O'$, đáy là đường tròn $\left( O \right)$ và có thể tích bằng $2\pi {{a}^{3}}$. Gọi $A$ và $B$ là hai điểm thuộc đường tròn $\left( O \right)$ sao cho $AB=a\sqrt{6}$. Khoảng cách từ tâm đường tròn đáy của khối nón đến mặt phẳng $\left( SAB \right)$ bằng
A. $\dfrac{\sqrt{6}a}{11}$.
B. $\dfrac{3\sqrt{6}a}{2}$.
C. $\dfrac{2\sqrt{33}a}{11}$.
D. $\dfrac{\sqrt{6}a}{3}$.
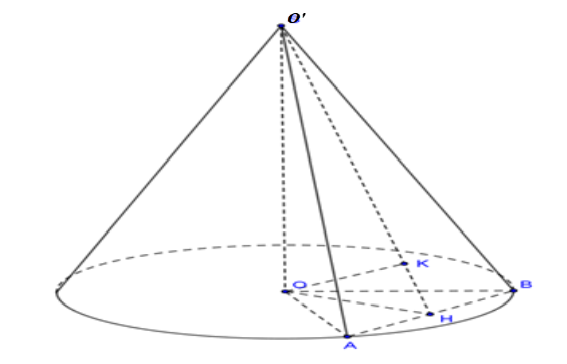Vì $O$ là tâm đường tròn đáy nên $\Rightarrow OA=OB=a\sqrt{3}$
Gọi $H$ là trung điểm của đoạn $AB$. Kẻ $OK\bot O'H$ $\left( K\in O'H \right)$.
Ta có $\left\{ \begin{aligned}
& AB\bot OH \\
& AB\bot O'O \\
\end{aligned} \right.$$\Rightarrow AB\bot \left( O'HO \right) $ $ \Rightarrow AB\bot OK$.
Do đó $\left\{ \begin{aligned}
& OK\bot AB \\
& OK\bot O'H \\
\end{aligned} \right.$$\Rightarrow OK\bot \left( O'AB \right) $ $ \Rightarrow d\left( O,\left( O'AB \right) \right)=OK$.
Ta thấy $AB=a\sqrt{6}=OA.\sqrt{2}$ $\Rightarrow \Delta OAB$ vuông cân tại $O$ $\Rightarrow OH=\dfrac{AB}{2}=\dfrac{a\sqrt{6}}{2}$.
Thể tích khối nón bằng: $V=\dfrac{1}{3}\pi O{{A}^{2}}.O'O$ $\Rightarrow O'O=\dfrac{3V}{\pi .O{{A}^{2}}}$ $=\dfrac{3.2\pi {{a}^{3}}}{\pi .3{{a}^{2}}}$ $=2a$.
Xét tam giác $O'HO$ vuông tại $O$ đường cao $OK$ ta có:
$OK=\dfrac{O'O.OH}{\sqrt{O'{{O}^{2}}+O{{H}^{2}}}}$ $=\dfrac{2a.\dfrac{a\sqrt{6}}{2}}{\sqrt{4{{a}^{2}}+\dfrac{6{{a}^{2}}}{4}}}$ $=\dfrac{2\sqrt{33}a}{11}$.
A. $\dfrac{\sqrt{6}a}{11}$.
B. $\dfrac{3\sqrt{6}a}{2}$.
C. $\dfrac{2\sqrt{33}a}{11}$.
D. $\dfrac{\sqrt{6}a}{3}$.
Gọi $H$ là trung điểm của đoạn $AB$. Kẻ $OK\bot O'H$ $\left( K\in O'H \right)$.
Ta có $\left\{ \begin{aligned}
& AB\bot OH \\
& AB\bot O'O \\
\end{aligned} \right.$$\Rightarrow AB\bot \left( O'HO \right) $ $ \Rightarrow AB\bot OK$.
Do đó $\left\{ \begin{aligned}
& OK\bot AB \\
& OK\bot O'H \\
\end{aligned} \right.$$\Rightarrow OK\bot \left( O'AB \right) $ $ \Rightarrow d\left( O,\left( O'AB \right) \right)=OK$.
Ta thấy $AB=a\sqrt{6}=OA.\sqrt{2}$ $\Rightarrow \Delta OAB$ vuông cân tại $O$ $\Rightarrow OH=\dfrac{AB}{2}=\dfrac{a\sqrt{6}}{2}$.
Thể tích khối nón bằng: $V=\dfrac{1}{3}\pi O{{A}^{2}}.O'O$ $\Rightarrow O'O=\dfrac{3V}{\pi .O{{A}^{2}}}$ $=\dfrac{3.2\pi {{a}^{3}}}{\pi .3{{a}^{2}}}$ $=2a$.
Xét tam giác $O'HO$ vuông tại $O$ đường cao $OK$ ta có:
$OK=\dfrac{O'O.OH}{\sqrt{O'{{O}^{2}}+O{{H}^{2}}}}$ $=\dfrac{2a.\dfrac{a\sqrt{6}}{2}}{\sqrt{4{{a}^{2}}+\dfrac{6{{a}^{2}}}{4}}}$ $=\dfrac{2\sqrt{33}a}{11}$.
Đáp án C.