Google
Câu hỏi: Cho hình trụ có hai đáy là hai hình tròn tâm $O, {O}'$, bán kính đáy bằng $a$, $AB$ là một dây cung của đường tròn $\left( O \right)$ sao cho tam giác ${O}'AB$ là tam giác đều và mặt phẳng $\left( {O}'AB \right)$ tạo với mặt phẳng chứa đường tròn $\left( O \right)$ một góc $60{}^\circ $. Khoảng cách từ điểm $O$ đến mặt phẳng $\left( {O}'AB \right)$ bằng
A. $\dfrac{a\sqrt{21}}{7}$.
B. $\dfrac{3a\sqrt{21}}{7}$.
C. $\dfrac{3a\sqrt{7}}{14}$.
D. $\dfrac{a\sqrt{21}}{14}$.
A. $\dfrac{a\sqrt{21}}{7}$.
B. $\dfrac{3a\sqrt{21}}{7}$.
C. $\dfrac{3a\sqrt{7}}{14}$.
D. $\dfrac{a\sqrt{21}}{14}$.
Chuẩn hóa $a=1$.
Gọi $\alpha $ là góc giữa mặt phẳng $\left( {O}'AB \right)$ và mặt phẳng chứa đường tròn $\left( O \right)$.
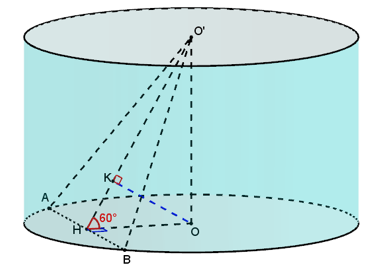
Gọi $H$ là trung điểm của $AB$.
Khi đó $OH\bot AB$ và $O{O}'\bot AB$, suy ra $AB\bot \left( O{O}'H \right)$ hay $\alpha =\widehat{{O}'HO}=60{}^\circ $.
Trong mặt phẳng $\left( {O}'OH \right)$, từ $O$ kẻ $OK\bot {O}'H$ tại $K$.
Suy ra $OK\bot \left( {O}'AB \right)\Rightarrow d\left( O,\left( {O}'AB \right) \right)=OK$.
Ta có: tam giác ${O}'AB$ là tam giác đều nên đặt ${O}'A={O}'B=AB=x, x>0$.
Xét tam giác ${O}'OH$ vuông tại $O$, ta có:
$\tan 60{}^\circ =\dfrac{O{O}'}{OH}\Leftrightarrow O{O}'=\sqrt{3}.OH\Leftrightarrow O{{{O}'}^{2}}=3O{{H}^{2}}\Leftrightarrow {{x}^{2}}-1=3\left( 1-\dfrac{{{x}^{2}}}{4} \right)\Leftrightarrow {{x}^{2}}=\dfrac{16}{7}\Leftrightarrow x=\dfrac{4}{\sqrt{7}}$.
Khi đó: $OH=\dfrac{\sqrt{21}}{7}; O{O}'=\dfrac{3\sqrt{7}}{7}$. Suy ra $OK=\dfrac{O{O}'.OH}{\sqrt{O{{{{O}'}}^{2}}+O{{H}^{2}}}}=\dfrac{\dfrac{\sqrt{21}}{7}.\dfrac{3\sqrt{7}}{7}}{\sqrt{\dfrac{3}{7}+\dfrac{9}{7}}}=\dfrac{3\sqrt{7}}{14}$.
Vậy $\text{d}\left( O,\left( {O}'AB \right) \right)=\dfrac{3a\sqrt{7}}{14}$.
Gọi $\alpha $ là góc giữa mặt phẳng $\left( {O}'AB \right)$ và mặt phẳng chứa đường tròn $\left( O \right)$.
Gọi $H$ là trung điểm của $AB$.
Khi đó $OH\bot AB$ và $O{O}'\bot AB$, suy ra $AB\bot \left( O{O}'H \right)$ hay $\alpha =\widehat{{O}'HO}=60{}^\circ $.
Trong mặt phẳng $\left( {O}'OH \right)$, từ $O$ kẻ $OK\bot {O}'H$ tại $K$.
Suy ra $OK\bot \left( {O}'AB \right)\Rightarrow d\left( O,\left( {O}'AB \right) \right)=OK$.
Xét tam giác ${O}'OH$ vuông tại $O$, ta có:
$\tan 60{}^\circ =\dfrac{O{O}'}{OH}\Leftrightarrow O{O}'=\sqrt{3}.OH\Leftrightarrow O{{{O}'}^{2}}=3O{{H}^{2}}\Leftrightarrow {{x}^{2}}-1=3\left( 1-\dfrac{{{x}^{2}}}{4} \right)\Leftrightarrow {{x}^{2}}=\dfrac{16}{7}\Leftrightarrow x=\dfrac{4}{\sqrt{7}}$.
Khi đó: $OH=\dfrac{\sqrt{21}}{7}; O{O}'=\dfrac{3\sqrt{7}}{7}$. Suy ra $OK=\dfrac{O{O}'.OH}{\sqrt{O{{{{O}'}}^{2}}+O{{H}^{2}}}}=\dfrac{\dfrac{\sqrt{21}}{7}.\dfrac{3\sqrt{7}}{7}}{\sqrt{\dfrac{3}{7}+\dfrac{9}{7}}}=\dfrac{3\sqrt{7}}{14}$.
Vậy $\text{d}\left( O,\left( {O}'AB \right) \right)=\dfrac{3a\sqrt{7}}{14}$.
Đáp án C.