Google
Câu hỏi: Cho hình trụ $\left( H \right)$ có hai đáy là hai đường tròn có tâm $O$ và $O'$, mặt phẳng $\left( \alpha \right)$ đi qua $O'$ và cắt đường tròn tâm $O$ tại hai điểm $A,B$ sao cho tam giác $O'AB$ là tam giác đều và có diện tích $\dfrac{{{a}^{2}}\sqrt{3}}{4}$. Biết góc giữa mp $\left( \alpha \right)$ và mp $\left( OAB \right)$ bằng ${{60}^{0}}$, tính khoảng cách từ điểm $O$ đến mặt phẳng $\left( {O}'AB \right)$ ?
A. $\dfrac{3a}{8}$
B. $\dfrac{a\sqrt{3}}{4}$.
C. $\dfrac{3a}{4}$.
D. $\dfrac{a\sqrt{3}}{8}$.
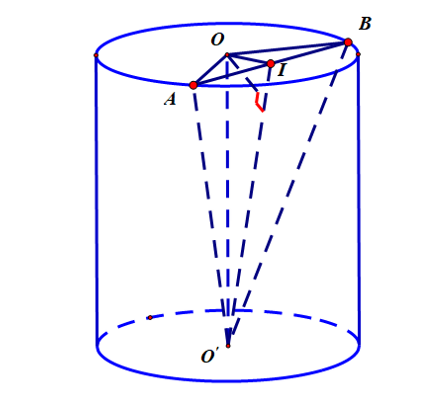$\Delta O'AB$ là tam giác đều và có diện tích $\dfrac{{{a}^{2}}\sqrt{3}}{4}$ $\Rightarrow AO'=AB=BO'=a$.
Gọi $I$ là trung điểm $AB$, $IO'=\dfrac{a\sqrt{3}}{2}$. Ta có: $\left\{ \begin{aligned}
& IO'\bot AB \\
& IO\bot AB \\
\end{aligned} \right.\Rightarrow \widehat{\left( \left( \alpha \right),\left( OAB \right) \right)}=\widehat{OIO'}={{60}^{0}}$.
$OO'=IO'.\sin {{60}^{0}}=\dfrac{3a}{4}$ ; $IA=\dfrac{AB}{2}=\dfrac{a}{2}$ ; $OI=IO'.\cos {{60}^{0}}=\dfrac{a\sqrt{3}}{4}$ ;
Gọi $d$ là khoảng cách từ điểm $O$ đến mặt phẳng $\left( {O}'AB \right)$
Ta có: $\dfrac{1}{{{d}^{2}}}=\dfrac{1}{O{{{{O}'}}^{2}}}+\dfrac{1}{O{{I}^{2}}}=\dfrac{16}{9{{a}^{2}}}+\dfrac{16}{3{{a}^{2}}}=\dfrac{64}{9{{a}^{2}}}$ $\Rightarrow d=\dfrac{3a}{8}$.
A. $\dfrac{3a}{8}$
B. $\dfrac{a\sqrt{3}}{4}$.
C. $\dfrac{3a}{4}$.
D. $\dfrac{a\sqrt{3}}{8}$.
Gọi $I$ là trung điểm $AB$, $IO'=\dfrac{a\sqrt{3}}{2}$. Ta có: $\left\{ \begin{aligned}
& IO'\bot AB \\
& IO\bot AB \\
\end{aligned} \right.\Rightarrow \widehat{\left( \left( \alpha \right),\left( OAB \right) \right)}=\widehat{OIO'}={{60}^{0}}$.
$OO'=IO'.\sin {{60}^{0}}=\dfrac{3a}{4}$ ; $IA=\dfrac{AB}{2}=\dfrac{a}{2}$ ; $OI=IO'.\cos {{60}^{0}}=\dfrac{a\sqrt{3}}{4}$ ;
Gọi $d$ là khoảng cách từ điểm $O$ đến mặt phẳng $\left( {O}'AB \right)$
Ta có: $\dfrac{1}{{{d}^{2}}}=\dfrac{1}{O{{{{O}'}}^{2}}}+\dfrac{1}{O{{I}^{2}}}=\dfrac{16}{9{{a}^{2}}}+\dfrac{16}{3{{a}^{2}}}=\dfrac{64}{9{{a}^{2}}}$ $\Rightarrow d=\dfrac{3a}{8}$.
Đáp án A.