Google
Câu hỏi: Cho hình chóp tứ giác đều $S.ABCD$ có góc giữa mặt phẳng chứa mặt bên và mặt phẳng đáy bằng $60{}^\circ $. Biết rằng mặt cầu ngoại tiếp hình chóp $S.ABCD$ có bán kính $R=\sqrt{3}.$ Tính thể tích của khối chóp $S.ABC$.
A. $\dfrac{576\sqrt{3}}{125}$.
B. $\dfrac{72\sqrt{3}}{125}$.
C. $\dfrac{288\sqrt{3}}{125}$.
D. $\dfrac{144\sqrt{3}}{125}$.
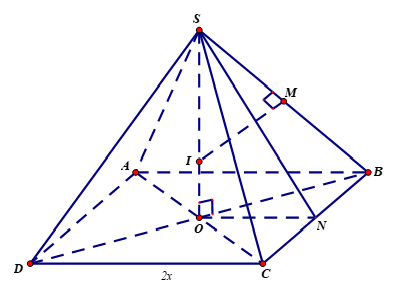Gọi $N$ là trung điểm cạnh $BC$ suy ra $\left( \left( SBC \right),\left( ABCD \right) \right)=\widehat{SNO}=60{}^\circ $.
Gọi $M$ là trung điểm cạnh $SB$, dựng $MI\bot SB$ $\left( I\in SO \right)$ suy ra $I$ là tâm mặt cầu ngoại tiếp khối chóp.
Đặt $DC=2x$. Khi đó, $SO=x\sqrt{3}$, $SB=x\sqrt{5}$.
Tam giác $SMI$ đồng dạng với tam giác $SOB$ suy ra $SI=\dfrac{SM.SB}{SO}=\dfrac{S{{B}^{2}}}{2SO}=\dfrac{5x\sqrt{3}}{6}=\sqrt{3}\Rightarrow x=\dfrac{6}{5}$ $\Rightarrow DC=\dfrac{12}{5},SO=\dfrac{6\sqrt{3}}{5}$.
Thể tích của khối chóp $S.ABC$ là $V=\dfrac{1}{3}SO.{{S}_{ABC}}=\dfrac{1}{3}.\dfrac{6\sqrt{3}}{5}.\dfrac{1}{2}{{\left( \dfrac{12}{5} \right)}^{2}}=\dfrac{144\sqrt{3}}{125}$.
A. $\dfrac{576\sqrt{3}}{125}$.
B. $\dfrac{72\sqrt{3}}{125}$.
C. $\dfrac{288\sqrt{3}}{125}$.
D. $\dfrac{144\sqrt{3}}{125}$.
Gọi $M$ là trung điểm cạnh $SB$, dựng $MI\bot SB$ $\left( I\in SO \right)$ suy ra $I$ là tâm mặt cầu ngoại tiếp khối chóp.
Đặt $DC=2x$. Khi đó, $SO=x\sqrt{3}$, $SB=x\sqrt{5}$.
Tam giác $SMI$ đồng dạng với tam giác $SOB$ suy ra $SI=\dfrac{SM.SB}{SO}=\dfrac{S{{B}^{2}}}{2SO}=\dfrac{5x\sqrt{3}}{6}=\sqrt{3}\Rightarrow x=\dfrac{6}{5}$ $\Rightarrow DC=\dfrac{12}{5},SO=\dfrac{6\sqrt{3}}{5}$.
Thể tích của khối chóp $S.ABC$ là $V=\dfrac{1}{3}SO.{{S}_{ABC}}=\dfrac{1}{3}.\dfrac{6\sqrt{3}}{5}.\dfrac{1}{2}{{\left( \dfrac{12}{5} \right)}^{2}}=\dfrac{144\sqrt{3}}{125}$.
Đáp án D.
