Google
Câu hỏi: Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a$, $SA=\sqrt{2}a$ vuông góc với đáy. Gọi $H, E, K$ lần lượt là hình chiếu vuông góc của $A$ lên $SB, SC, SD$. Khối nón có đường tròn đáy là đường tròn ngoại tiếp tam giác $HKE$ và có đỉnh thuộc mặt phẳng $\left( ABCD \right)$ có thể tích bằng
A. $\dfrac{\pi {{a}^{3}}}{24}$.
B. $\dfrac{\pi {{a}^{3}}}{12}$.
C. $\dfrac{\pi {{a}^{3}}}{8}$.
D. $\dfrac{\pi {{a}^{3}}}{6}$.
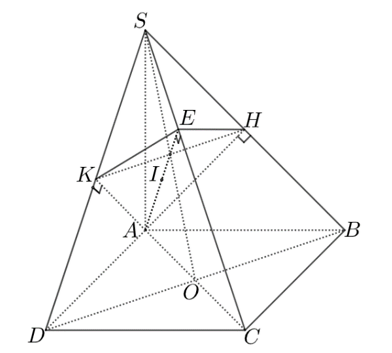Gọi $O=AC\cap BD$ ; $I$ là trung điểm $AE$.
Dễ dàng chứng minh được: $AK\bot \left( SCD \right);AH\bot \left( SBC \right);SC\bot \left( AKH \right);SC\bot \left( AKE \right)$
$\Rightarrow \left( AKH \right)\equiv \left( AKE \right)$ $\Rightarrow $ $A, K, E, H$ cùng thuộc 1 mặt phẳng.
Ta có: $AK\bot \left( SCD \right)\Rightarrow \left\{ \begin{aligned}
& AK\bot KE \\
& AK\bot KC \\
\end{aligned} \right.;AH\bot \left( SBC \right)\Rightarrow \left\{ \begin{aligned}
& AH\bot HE \\
& AH\bot HC \\
\end{aligned} \right.$.
$\Rightarrow \widehat{AKE}+\widehat{AHE}={{180}^{0}}$ $\Rightarrow $ Tứ giác $AKEH$ nội tiếp đường tròn đường kính $AE$, có tâm $I$ là trung điểm $AE$.
Ta có: $\widehat{AKC}=\widehat{AEC}=\widehat{AHC}={{90}^{0}}$ $\Rightarrow KO=EO=HO=\dfrac{AC}{2}$.
$\Rightarrow OI\bot \left( HKE \right)$ $\Rightarrow $ Khối nón cần tìm có đỉnh là $O$, đường cao là $OI$, bán kính đáy $R=AI=\dfrac{AE}{2}$.
Ta có: $AC=a\sqrt{2};AE=\sqrt{\dfrac{S{{A}^{2}}.A{{C}^{2}}}{S{{A}^{2}}+A{{C}^{2}}}}=\sqrt{\dfrac{2{{a}^{2}}.2{{a}^{2}}}{2{{a}^{2}}+2{{a}^{2}}}}=a$ $\Rightarrow R=\dfrac{a}{2}$.
$h=OI=\sqrt{A{{O}^{2}}-A{{I}^{2}}}=\sqrt{{{\left( \dfrac{AC}{2} \right)}^{2}}-A{{I}^{2}}}=\sqrt{{{\left( \dfrac{a\sqrt{2}}{2} \right)}^{2}}-{{\left( \dfrac{a}{2} \right)}^{2}}}=\dfrac{a}{2}$.
Thể tích của khối nón cần tìm là: $V=\dfrac{1}{3}.\pi {{R}^{2}}h=\dfrac{1}{3}\pi .{{\left( \dfrac{a}{2} \right)}^{2}}.\dfrac{a}{2}=\dfrac{\pi {{a}^{3}}}{24}$.
A. $\dfrac{\pi {{a}^{3}}}{24}$.
B. $\dfrac{\pi {{a}^{3}}}{12}$.
C. $\dfrac{\pi {{a}^{3}}}{8}$.
D. $\dfrac{\pi {{a}^{3}}}{6}$.
Dễ dàng chứng minh được: $AK\bot \left( SCD \right);AH\bot \left( SBC \right);SC\bot \left( AKH \right);SC\bot \left( AKE \right)$
$\Rightarrow \left( AKH \right)\equiv \left( AKE \right)$ $\Rightarrow $ $A, K, E, H$ cùng thuộc 1 mặt phẳng.
Ta có: $AK\bot \left( SCD \right)\Rightarrow \left\{ \begin{aligned}
& AK\bot KE \\
& AK\bot KC \\
\end{aligned} \right.;AH\bot \left( SBC \right)\Rightarrow \left\{ \begin{aligned}
& AH\bot HE \\
& AH\bot HC \\
\end{aligned} \right.$.
$\Rightarrow \widehat{AKE}+\widehat{AHE}={{180}^{0}}$ $\Rightarrow $ Tứ giác $AKEH$ nội tiếp đường tròn đường kính $AE$, có tâm $I$ là trung điểm $AE$.
Ta có: $\widehat{AKC}=\widehat{AEC}=\widehat{AHC}={{90}^{0}}$ $\Rightarrow KO=EO=HO=\dfrac{AC}{2}$.
$\Rightarrow OI\bot \left( HKE \right)$ $\Rightarrow $ Khối nón cần tìm có đỉnh là $O$, đường cao là $OI$, bán kính đáy $R=AI=\dfrac{AE}{2}$.
Ta có: $AC=a\sqrt{2};AE=\sqrt{\dfrac{S{{A}^{2}}.A{{C}^{2}}}{S{{A}^{2}}+A{{C}^{2}}}}=\sqrt{\dfrac{2{{a}^{2}}.2{{a}^{2}}}{2{{a}^{2}}+2{{a}^{2}}}}=a$ $\Rightarrow R=\dfrac{a}{2}$.
$h=OI=\sqrt{A{{O}^{2}}-A{{I}^{2}}}=\sqrt{{{\left( \dfrac{AC}{2} \right)}^{2}}-A{{I}^{2}}}=\sqrt{{{\left( \dfrac{a\sqrt{2}}{2} \right)}^{2}}-{{\left( \dfrac{a}{2} \right)}^{2}}}=\dfrac{a}{2}$.
Thể tích của khối nón cần tìm là: $V=\dfrac{1}{3}.\pi {{R}^{2}}h=\dfrac{1}{3}\pi .{{\left( \dfrac{a}{2} \right)}^{2}}.\dfrac{a}{2}=\dfrac{\pi {{a}^{3}}}{24}$.
Đáp án A.