Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh bằng $a$...

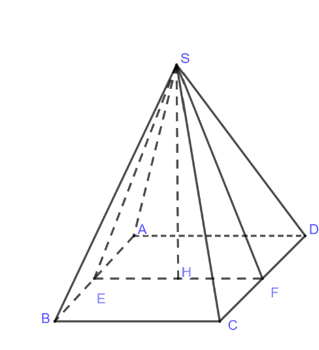Gọi $E,F$ lần lượt là trung điểm của $AB,CD$
Do $\Delta SAB$ đều cạnh $a$ nên $SE\bot AB$ (1) và $SE=\dfrac{a\sqrt{3}}{2}$
$\Delta SCD$ vuông cân tại $S$ nên $SF\bot CD$ và $SF=\dfrac{1}{2}CD=\dfrac{a}{2}$
Ta có $\left\{ \begin{aligned}
& AB\text{//CD} \\
& CD\bot SF \\
\end{aligned} \right.\Rightarrow AB\bot SF$ (2)
Từ (1) và (2) $\Rightarrow AB\bot \left( SEF \right)\Rightarrow \left( ABCD \right)\bot \left( SEF \right)$ theo giao tuyến $EF$
Trong $\left( SEF \right)$ kẻ $SH\bot EF$ khi đó $SH\bot \left( ABCD \right)$ tại $H$
$\Rightarrow $ $SH$ là bán kính mặt cầu có tâm $S$ và tiếp xúc với mặt phẳng $(ABCD)$
Ta có $EF=BC=a$
Xét $\Delta SEF$ có $S{{E}^{2}}+S{{F}^{2}}=\dfrac{3{{a}^{2}}}{4}+\dfrac{{{a}^{2}}}{4}={{a}^{2}}=E{{F}^{2}}\Rightarrow \Delta SEF$ vuông tại $S$
Do đó $\dfrac{1}{S{{H}^{2}}}=\dfrac{1}{S{{E}^{2}}}+\dfrac{1}{S{{F}^{2}}}=\dfrac{4}{3{{a}^{2}}}+\dfrac{4}{{{a}^{2}}}=\dfrac{16}{3{{a}^{2}}}\Rightarrow SH=\dfrac{\sqrt{3}a}{4}$
Vậy diện tích mặt cầu có tâm $S$ và tiếp xúc với mặt phẳng $(ABCD)$ bằng
$S=4\pi {{R}^{2}}=4\pi {{\left( \dfrac{\sqrt{3}a}{4} \right)}^{2}}=\dfrac{3}{4}\pi {{a}^{2}}$.